On the basis of question we draw a figure of a circle with centre in which two chords AB and CD intersect each other at the point P

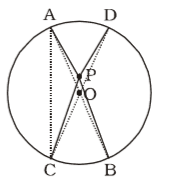
Given that , ∠AOD = 20° and ∠BOC = 30°
∠BOC = 2 ∠BAC
∠AOD = 2 ∠DCA
∴ ∠BOC + ∠AOD = 2 (∠BAC + ∠DCA)

Correct Option: C

On the basis of question we draw a figure of a circle with centre in which two chords AB and CD intersect each other at the point P

Given that , ∠AOD = 20° and ∠BOC = 30°
∠BOC = 2 ∠BAC
∠AOD = 2 ∠DCA
∴ ∠BOC + ∠AOD = 2 (∠BAC + ∠DCA)
∠BOC + ∠AOD = 2 ∠BPC (Exterior angles' sum)
∴ 2∠BPC = 20° + 30° = 50°
⇒ ∠BPC = 25°

As per the given in question , we draw a figure of a ∆ABC,

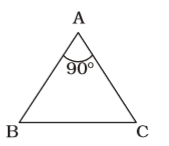
Here , AB² + AC² = BC² and BC = √2AB,
AB² + AC² = BC² ⇒ ∠BAC = 90°

Correct Option: B

As per the given in question , we draw a figure of a ∆ABC,

Here , AB² + AC² = BC² and BC = √2AB,
AB² + AC² = BC² ⇒ ∠BAC = 90°
⇒ AB² + AC² = 2AB²
⇒ AB² = AC²
⇒ AB = AC
∴ ∠ABC = ∠ACB = 45°

On the basis of question we draw a figure of a ∆ABC in which a straight line parallel to BC intersects AB and AC at points P and Q respectively.

Given , AP = QC, PB= 4 units and AQ = 9 units
PQ || BC

Correct Option: C

On the basis of question we draw a figure of a ∆ABC in which a straight line parallel to BC intersects AB and AC at points P and Q respectively.

Given , AP = QC, PB= 4 units and AQ = 9 units
PQ || BC

According to question , we draw a figure ofa circle with centre O and AB and CD are two chords

Here , ∠ AOC = 50°, ∠ BOD = 40°
Join CB.
∠AOC + ∠BOD = 2∠ABC + 2∠BCD (Exterior angles of triangle)
∠AOC + ∠BOD = 2(∠ABC + ∠BCD) = 2∠BPD

Correct Option: C

According to question , we draw a figure ofa circle with centre O and AB and CD are two chords

Here , ∠ AOC = 50°, ∠ BOD = 40°
Join CB.
∠AOC + ∠BOD = 2∠ABC + 2∠BCD (Exterior angles of triangle)
∠AOC + ∠BOD = 2(∠ABC + ∠BCD) = 2∠BPD

According to question ,
Error = 45°27' – 45° = 27'
We have, 60' = 1°

Correct Option: B

According to question ,
Error = 45°27' – 45° = 27'
We have, 60' = 1°