Plane Geometry
- The length of the tangent drawn to a circle of radius 4 cm from a point 5 cm away from the centre of the circle is
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a circle with centre O ,

∠OBA = 90°
Given that , OA = 5, OB = 4
∴ AB = √OA² - OB²Correct Option: A
According to question , we draw a figure of a circle with centre O ,

∠OBA = 90°
Given that , OA = 5, OB = 4
∴ AB = √OA² - OB²
AB = √25 - 16
AB = √9 = 3 cm
- Two circles intersect at A and B. P is a point on produced BA. PT and PQ are tangents to the circles. The relation of PT and PQ is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of two circles intersect at A and B ,

PT = PQCorrect Option: D
As per the given in question , we draw a figure of two circles intersect at A and B ,

PT = PQ
Hence , Tangents will be equal.
- P and Q are two points on a circle with centre at O. R is a point on the minor arc of the circle, between the points P and Q. The tangents to the circle at the points P and Q meet each other at the point S. If ∠PSQ = 20°, then ∠PRQ = ?
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a circle with centre O ,
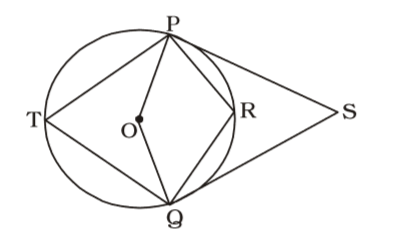
∠OPS = ∠OQS = 90°
Given , ∠PSQ = 20°;
∴ ∠POQ = 160°
[∠PSQ + ∠POQ = 180°]Correct Option: D
According to question , we draw a figure of a circle with centre O ,

∠OPS = ∠OQS = 90°
Given , ∠PSQ = 20°;
∴ ∠POQ = 160°
[∠PSQ + ∠POQ = 180°]
⇒ ∠PTQ = 80°
PRQT is a concyclic quadrilateral.
∴ ∠PRQ = 180° – 80° = 100°
- The radii of two circles are 5cm and 3cm, the distance between their centre is 24 cm. Then the length of the transverse common tangent is
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of two circles with radii 5cm and 3cm ,

Here , d = 24 cm
We know that , Transverse common tangent = √d² - (r1 +r2)²
Transverse common tangent = √(24)² - (5 + 3)⊃
Transverse common tangent = √576 - 64Correct Option: C
On the basis of question we draw a figure of two circles with radii 5cm and 3cm ,

Here , d = 24 cm
We know that , Transverse common tangent = √d² - (r1 +r2)²
Transverse common tangent = √(24)² - (5 + 3)⊃
Transverse common tangent = √576 - 64
Transverse common tangent = √512
Transverse common tangent = 16√2cm.
- The distance between the centre of two equal circles, each of radius 3 cm, is 10 cm. The length of a transverse common tangent is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of two equal circles with centres X and Y ,

We know that , Transverse common tangent = √(Distance between centres)² - (r1 +r2)²Correct Option: A
As per the given in question , we draw a figure of two equal circles with centres X and Y ,

We know that , Transverse common tangent = √(Distance between centres)² - (r1 +r2)²
Transverse common tangent = √10² - 6² = √16 × 4
Transverse common tangent = 8 cm

