Plane Geometry
- We have an angle of 21°/2 .How big it will look through a glass that magnifies things three times?
-
View Hint View Answer Discuss in Forum
Measure of the angle will not change.
Correct Option: D
Measure of the angle will not change.Hence required answer will be option D .
i.e. 2 1° × 5 2
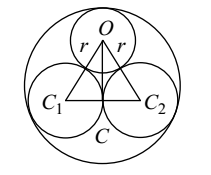
- Two circles of unit radius touch each other and each of them touches internally a circle of radius two, as shown in the following figure. The radius of the circle which thouches all the three circles:
-
View Hint View Answer Discuss in Forum
From given figure , we can see that
CC1 = 1, OC1 = 1 + r
OC = AC – AO = CD – AO = 2 – r [ AC and CD are the radii of the bigger circle ]
∴ (OC1)2 = (CC1)2 + (OC)2
⇒ (1 + r)2 = 12 + (2 - r)2
⇒ 1 + r2 + 2r = 1 + 4 + r2 - 4r
⇒ 2r + 4r = 4
⇒ 6r = 4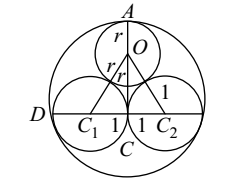
Correct Option: C
From given figure , we can see that
CC1 = 1, OC1 = 1 + r
OC = AC – AO = CD – AO = 2 – r [ AC and CD are the radii of the bigger circle ]
∴ (OC1)2 = (CC1)2 + (OC)2
⇒ (1 + r)2 = 12 + (2 - r)2
⇒ 1 + r2 + 2r = 1 + 4 + r2 - 4r ⇒ 2r + 4r = 4 ⇒ 6r = 4⇒ r = 2 3 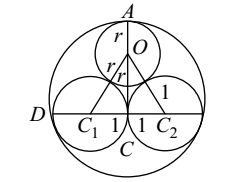
- If, in the following figure, PA = 8 cm, PD = 4 cm, CD equal to 3 cm, then AB is :

-
View Hint View Answer Discuss in Forum
From above given figure , we have
PA = 8 cm, PD = 4 cm and CD = 3 cm , PC = PD + CD = 4 + 3 = 7 cm
we know that , PA X PB = PC X PD
⇒ 8 x PB = 7 x 4 ⇒ 2 x PB = 7Correct Option: D
From above given figure , we have
PA = 8 cm, PD = 4 cm and CD = 3 cm , PC = PD + CD = 4 + 3 = 7 cm
we know that , PA X PB = PC X PD
⇒ 8 x PB = 7 x 4 ⇒ 2 x PB = 7⇒ PB = 7 = 3.5 cm 2
∴ AB = PA - PB = 8 - 3.5 = 4.5 cm
- In the given figure, what is the length of AD in terms of b and c :
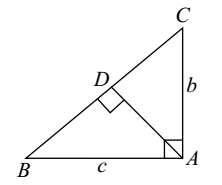
-
View Hint View Answer Discuss in Forum
In right angle triangle , we know that
Area of triangle = 1 base x height 2 ar(∆ABC) = 1 bc ............. ( 1 ) 2 ar(∆ABC) = 1 BC × AD = 1 √b2+c2× AD ............. ( 2 ) 2 2 Correct Option: D
In right angle triangle , we know that
Area of triangle = 1 base x height 2 ar(∆ABC) = 1 bc ............. ( 1 ) 2 ar(∆ABC) = 1 BC × AD = 1 √b2+c2× AD ............. ( 2 ) 2 2
[ By pythagorus theorem , ∴ BC2 = b2 + c2]∴ 1 √b2+c2× AD = 1 bc ⇒ AD = bc 2 2 √b2+c2
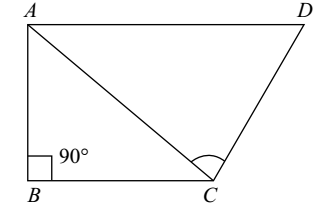
- In a quadrilateral ABCD, ∠B = 90° and AD2 = AB2 + BC2 + CD2, then ∠ACD is equal to:
-
View Hint View Answer Discuss in Forum
In a quadrilateral ABCD,
Given :- ∠B = 90°
AB2 + BC2 + CD2 = AC2 + CD2 = AD2 { ∴ In triangle ABC , AB2 + BC2 = AC2 }
Correct Option: A
In a quadrilateral ABCD,
Given :- ∠B = 90°
AB2 + BC2 + CD2 = AC2 + CD2 = AD2 { ∴ In triangle ABC , AB2 + BC2 = AC2 }
So, in triangle ACD, angle opposite to AD = 90° ( by Converse of Pythagoras theorem)
⇒ ∠ACD = 90°