Plane Geometry
- In ∆ ABC, ∠A + ∠B = 65°, ∠B + ∠C = 140°, then find ∠B.
-
View Hint View Answer Discuss in Forum
According to question ,
Given , ∠ A + ∠ B = 65°
In ∆ ABC,
As we know that , ∠ A + ∠ B + ∠ C = 180°
∴ ∠ C = 180° – 65° = 115°
and ∠ B + ∠ C = 140°Correct Option: B
According to question ,
Given , ∠ A + ∠ B = 65°
In ∆ ABC,
As we know that , ∠ A + ∠ B + ∠ C = 180°
∴ ∠ C = 180° – 65° = 115°
and ∠ B + ∠ C = 140°
⇒ ∠ B + 115° = 140°
∴ ∠ B = 140° – 115° = 25°
- In a ∆ ABC, AB = AC and BA is produced to D such that AC = AD. Then the ∠ BCD is
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a triangle ABC

Let ∠ ABC = ∠ ACB = y [∵AB = AC]
∴ ∠ BAC = 180° – 2y
⇒ ∠CAD = 180° – 2y
Also, ∠BAD = 180°Correct Option: D
According to question , we draw a figure of a triangle ABC

Let ∠ ABC = ∠ ACB = y [∵AB = AC]
∴ ∠ BAC = 180° – 2y
⇒ ∠CAD = 180° – 2y
Also, ∠BAD = 180°
∴ 180° = (180° – 2y) × 2
⇒ 180° – 2y = 90°
⇒ 2y = 90° = ∠ BCD
- In triangle ABC, ∠ BAC = 75°, ∠ABC = 45°.BC is produced to D. If ∠ ACD = x°, then x/3 % of 60° is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of a triangle ABC
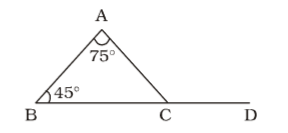
Given that , ∠ BAC = 75°, ∠ABC = 45° , ∠ ACD = x°
As we know that sum of three angles of triangle is 180°
∠ ACB = 180° – 75° – 45° = 60°
∠ ACD = 180° – 60° = 120° = xCorrect Option: D
As per the given in question , we draw a figure of a triangle ABC

Given that , ∠ BAC = 75°, ∠ABC = 45° , ∠ ACD = x°
As we know that sum of three angles of triangle is 180°
∠ ACB = 180° – 75° – 45° = 60°
∠ ACD = 180° – 60° = 120° = x∴ x % of 60° = 60 × 120 = 24° 3 300
- In a ∆ ABC ∠A : ∠B : ∠C = 2 : 3 : 4. A line CD drawn || to AB, then the ∠ACD is :
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of ∆ ABC
Given , ∠A : ∠B : ∠C = 2 : 3 : 4
Let ∠A = 2y , ∠B = 3y , ∠C = 4y
In ∆ ABC ,
We know that , 2y + 3y + 4y = 180°
⇒ 9y = 180°
⇒ y = 20°
∴ Angles of triangle are 40°, 60° and 80°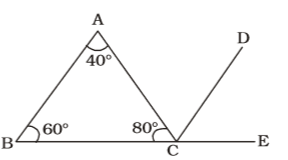
AB || CDCorrect Option: B
According to question , we draw a figure of ∆ ABC
Given , ∠A : ∠B : ∠C = 2 : 3 : 4
Let ∠A = 2y , ∠B = 3y , ∠C = 4y
In ∆ ABC ,
We know that , 2y + 3y + 4y = 180°
⇒ 9y = 180°
⇒ y = 20°
∴ Angles of triangle are 40°, 60° and 80°
AB || CD
∠DCE = ∠ABC = 60°
∴ ∠ACB + ∠ACD + ∠DCE = 180°
⇒ ∠ACD = 180° – 120° = 60°
- Two chords AB, CD of a circle with centre O intersect each other at P. ∠ADP = 23° and ∠APC = 70°, then the ∠BCD is
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of a circle with centre O

∠APC = 70° = ∠DPB
∴ ∠APD = 180° – 70° = 110° = ∠BPC
Also, ∠ADC = ∠ABC = 23°Correct Option: B
On the basis of question we draw a figure of a circle with centre O

∠APC = 70° = ∠DPB
∴ ∠APD = 180° – 70° = 110° = ∠BPC
Also, ∠ADC = ∠ABC = 23°
∴ ∠BCD = 180° –110° – 23°= 47°

