Plane Geometry
- I and O are respectively the in-centre and circumcentre of a triangle ABC. The line AI produced intersects the circumcircle of ∆ ABC at the point D.
If ∠ABC = x°, ∠BID = y° and ∠BOD = z°, then z + x = y
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of triangle ABC in which I and O are respectively the in-centre and circumcentre
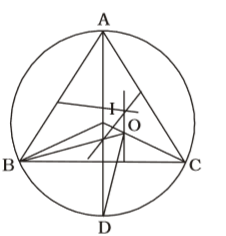
Given that , ∠ABC = x°, ∠BID = y° and ∠BOD = z°
OA = OB = OC
∠BID = ∠ABC
⇒ x = y
∠BOD = 2 ∠BADCorrect Option: A
According to question , we draw a figure of triangle ABC in which I and O are respectively the in-centre and circumcentre

Given that , ∠ABC = x°, ∠BID = y° and ∠BOD = z°
OA = OB = OC
∠BID = ∠ABC
⇒ x = y
∠BOD = 2 ∠BAD∴ z + x = 3y = 3 y y
- The length of radius of a circumcircle of a triangle having sides 3cm, 4cm and 5cm is :
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of a circumcircle of a triangle

We know that , 3² + 4² = 5² [Pythagorean Triplet]
∆ ABC is a right angled triangle.
∠B = 90° = angle at the circumferenceCorrect Option: B
As per the given in question , we draw a figure of a circumcircle of a triangle

We know that , 3² + 4² = 5² [Pythagorean Triplet]
∆ ABC is a right angled triangle.
∠B = 90° = angle at the circumference
Since, Diameter of circle = 5 cm
∴ Circum-radius = 5 ÷ 2 = 2.5 cm
- The length of the two sides forming the right angle of a right-angled triangle are 6 cm and 8 cm. The length of its circum-radius is :
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of a right-angled triangle whose two sides are 6 cm and 8 cm
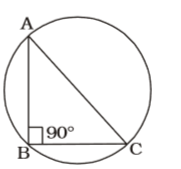
∠ABC = 90°
AC = Diameter of circle
From ∆ABC ,
∴ AC = √AB² + BC²Correct Option: A
On the basis of question we draw a figure of a right-angled triangle whose two sides are 6 cm and 8 cm

∠ABC = 90°
AC = Diameter of circle
From ∆ABC ,
∴ AC = √AB² + BC²
∴ AC = √6² + 8² = √36 + 64
AC = √100 = 10 cm
∴ Circum-radius = AC / 2 = 5 cm
- AC is the diameter of a circumcircle of ∆ ABC. Chord ED is parallel to the diameter AC. If ∠CBE = 50°, then the measure of ∠DEC is
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure circle and chord ED is parallel to the diameter AC
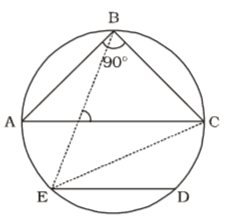
∠CBE = 50°
∠BAC + ∠BCA = 90° [∵ ∠ABC = 90°]
∠ABE = 90° – 50° = 40°Correct Option: D
According to question , we draw a figure circle and chord ED is parallel to the diameter AC

∠CBE = 50°
∠BAC + ∠BCA = 90° [∵ ∠ABC = 90°]
∠ABE = 90° – 50° = 40°
∴ ∠ABE = ∠ACE = 40°
∴ ∠ACE = ∠DEC = 40°
- A circle has its centre at O. A tangent drawn from a point P, which is situated outside the circle, touches the circle at A. If PA = 4 cm and PO = 5 cm, then the length of the radius of the circle is
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure circle with centre O in which a tangent drawn from a point P
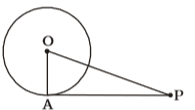
OA ⊥ AP
Here , OP = 5 cm.
PA = 4 cm.
From ∆AOP ,
∴ OA = √OP² - AP²Correct Option: C
According to question , we draw a figure circle with centre O in which a tangent drawn from a point P

OA ⊥ AP
Here , OP = 5 cm.
PA = 4 cm.
From ∆AOP ,
∴ OA = √OP² - AP²
OA = √5² - 4² = √25 - 16
OA = √9 = 3 cm.

