Plane Geometry
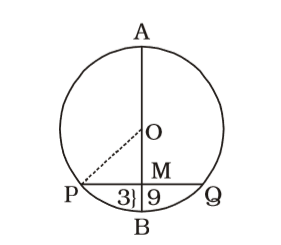
- In a given circle, the chord PQ is of length 18 cm. AB is the perpendicular bisector of PQ at M. If MB = 3 cm, then the length of AB is
-
View Hint View Answer Discuss in Forum
As per the given figure in question ,

Here , PQ = 18 cm
PM = MQ = 9 cm
OP = OB = r cm
MB = 3 cm
From ∆ OPM,
OP² = PM² + OM²
⇒ r² = 9² + (r – 3)²
⇒ r² = 81 + r² – 6r + 9
⇒ 81 – 6r + 9 = 0Correct Option: B
As per the given figure in question ,

Here , PQ = 18 cm
PM = MQ = 9 cm
OP = OB = r cm
MB = 3 cm
From ∆ OPM,
OP² = PM² + OM²
⇒ r² = 9² + (r – 3)²
⇒ r² = 81 + r² – 6r + 9
⇒ 81 – 6r + 9 = 0
⇒ 6r = 90
⇒ r = 15 cm
∴ AB = 2r = 30 cm
- Three circles of radius 6 cm each touches each other externally. Then the distance of the centre of one circle from the line joining the centres of other two circles is equal to
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of three circles of radius 6 cm each touches each other externally ,
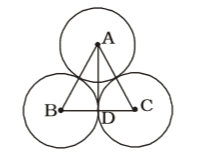
ABC will be an equilateral triangle whose each side = 12 cm.
AD ⊥ BC
∴ BD = DC = 6 cm.
AD ⊥ BC
∴ AD = √AB² - BD²
AD= √12² - 6²
AD = √(12 + 6)(12 - 6)Correct Option: B
According to question , we draw a figure of three circles of radius 6 cm each touches each other externally ,

ABC will be an equilateral triangle whose each side = 12 cm.
AD ⊥ BC
∴ BD = DC = 6 cm.
AD ⊥ BC
∴ AD = √AB² - BD²
AD= √12² - 6²
AD = √(12 + 6)(12 - 6)
AD = √18 × 6 = 6√3 cm.
- Chords PQ and RS of a circle, when produced, meet at a point O. If PQ = 6 cm, OQ = 8 cm and OS = 7 cm, then length (in cm) of the chord RS is
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of Chords PQ and RS of a circle, when produced, meet at a point O ,
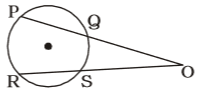
Given that , PQ = 6 cm, OQ = 8 cm and OS = 7 cm
We know that , OP × OQ = OS × OR
⇒ (6 + 8) × 8 = 7 × ORCorrect Option: D
On the basis of question we draw a figure of Chords PQ and RS of a circle, when produced, meet at a point O ,

Given that , PQ = 6 cm, OQ = 8 cm and OS = 7 cm
We know that , OP × OQ = OS × OR
⇒ (6 + 8) × 8 = 7 × OR⇒ OR = 14 × 8 = 16 cm. 7
∴ RS = OR – OS = 16 – 7 = 9 cm.
- Let O be the centre of a circle. A, B, C and D are four points on the circumference of the circle in the given order, such that ∠AOC = 130°. Then the measure of ∠ABC and ∠ADC are respectively.
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a circle with centre O ,

As we know that Angle subtended by an arc at the centre is twice to that subtended at the circumference.Correct Option: B
According to question , we draw a figure of a circle with centre O ,

As we know that Angle subtended by an arc at the centre is twice to that subtended at the circumference.
∴ ∠ABC = ∠ADC = 130° ÷ 2 = 65°
- Chords AB and CD of a circle intersect at E. If AE = 9 cm, BE = 12 cm and CE = 3DE, then the length of DE (in cm) is
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of a circle in which chords AB and CD intersect at E ,
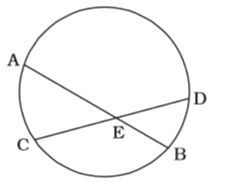
Given , AE = 9 cm, BE = 12 cm and CE = 3DE
Using theorem,
CE × ED = AE × EB
⇒ 3 DE × DE = 9 × 12Correct Option: C
On the basis of question we draw a figure of a circle in which chords AB and CD intersect at E ,

Given , AE = 9 cm, BE = 12 cm and CE = 3DE
Using theorem,
CE × ED = AE × EB
⇒ 3 DE × DE = 9 × 12⇒ DE² = 9 × 12 = 36 3
⇒ DE = √36 = 6 cm.

