Plane Geometry
- In triangle PQR, points A, B and C are taken on PQ, PR and QR respectively such that QC = AC and CR = CB. If ∠QPR = 40°, then ∠ACB is equal to :
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a triangle PQR in which points A, B and C are taken on PQ, PR and QR respectively

Given that , ∠QPR = 40°
AC = QC
∴ ∠QAC = ∠CQA = y ( say )
CR = CB
∴ ∠ CBR = ∠CRB = z
∴ From ∆ PQR,
∠y + ∠z + 40° = 180°
∠y + ∠z = 140° ......(i)Correct Option: D
According to question , we draw a figure of a triangle PQR in which points A, B and C are taken on PQ, PR and QR respectively

Given that , ∠QPR = 40°
AC = QC
∴ ∠QAC = ∠CQA = y ( say )
CR = CB
∴ ∠ CBR = ∠CRB = z
∴ From ∆ PQR,
∠y + ∠z + 40° = 180°
∠y + ∠z = 140° ......(i)
Again, ∠ ACQ + ∠ ACB + ∠ BCR = 180°
⇒ 180° – 2y + ∠ ACB + 180° – 2z = 180°
⇒ ∠ ACB = 2 (y + z) – 180° = 2 × 140 – 180° = 100°
- Internal bisectors of angles ∠B and ∠C of a triangle ABC meet at O. If ∠BAC = 80°, then the value of ∠BOC is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of a triangle ABC in which ∠B and ∠C are internal bisectors of angles of triangle

Here , ∠BAC = 80°
In ∆ ABC ,
As we know that , ∠A + ∠B + ∠C = 180°
∴ ∠B + ∠C = 180° – 80° = 100°∠B + ∠C = 50° 2 2
Correct Option: D
As per the given in question , we draw a figure of a triangle ABC in which ∠B and ∠C are internal bisectors of angles of triangle

Here , ∠BAC = 80°
In ∆ ABC ,
As we know that , ∠A + ∠B + ∠C = 180°
∴ ∠B + ∠C = 180° – 80° = 100°∠B + ∠C = 50° 2 2
In ∆ BOC ,
⇒ ∠OBC + ∠OCB = 50°
∴ ∠BOC = 180° – 50° = 130°
- O is the centre and arc ABC subtends an angle of 130° at O. AB is extended to P. Then ∠PBC is
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of a circle with centre O and arc ABC subtends an angle of 130° at O ,
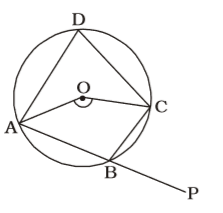
Given that , ∠AOC = 130°⇒ ∠ADC = 1 × 130° = 65° 2
Correct Option: C
On the basis of question we draw a figure of a circle with centre O and arc ABC subtends an angle of 130° at O ,

Given that , ∠AOC = 130°⇒ ∠ADC = 1 × 130° = 65° 2
∠PBC = ∠ADC = 65°
- In ∆ ABC, draw BE ⊥ AC and CF ⊥ AB and the perpendicular BE and CF intersect at the point O. If ∠ BAC = 70°, then the value of ∠ BOC is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of a triangle ABC and BE ⊥ AC and CF ⊥ AB and the perpendicular BE and CF intersect at the point O
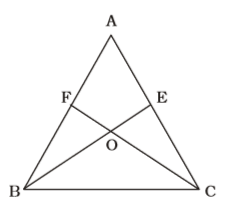
Here , ∠BAC = 70°
∠ABC + ∠ACB = 110° ...(i)
From ∠BCF,
∠CFB + ∠FBC + ∠FCB = 180°
⇒ ∠FBC + ∠FCB = 90° ...(ii)
From ∆ BCE,Correct Option: D
As per the given in question , we draw a figure of a triangle ABC and BE ⊥ AC and CF ⊥ AB and the perpendicular BE and CF intersect at the point O

Here , ∠BAC = 70°
∠ABC + ∠ACB = 110° ...(i)
From ∠BCF,
∠CFB + ∠FBC + ∠FCB = 180°
⇒ ∠FBC + ∠FCB = 90° ...(ii)
From ∆ BCE,
∠ECB + ∠EBC = 90° ...(iii)
From (ii) + (iii) – (i) , we get
⇒ ∠EBC + ∠FCB = 180° – 110° = 70°
∴ ∠BOC = 180° – 70° = 110°
- The angle between the external bisectors of two angles of a triangle is 60°. Then the third angle of the triangle is
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a external bisector triangle ABC

Given , ∠BOC = 60°
∠ABC + ∠CBP = 180°
⇒ ∠B + 2 ∠1 = 180°
⇒ 2∠1 = 180° – ∠B⇒ ∠1 = 90° – 1 ∠B ........( 1 ) 2
∠B Again, ∠ACB + ∠QCB = 180°⇒ ∠2 = 90° – 1 ∠C ...........( 2 ) 2
In ∆ BOC,
∠1 + ∠2 +∠BOC = 180°⇒ 90° - 1 ∠B + 90° - 1 ∠C + ∠BOC = 180° { ∴ Using ( 1) and ( 2 ) } 2 2
Correct Option: C
According to question , we draw a figure of a external bisector triangle ABC

Given , ∠BOC = 60°
∠ABC + ∠CBP = 180°
⇒ ∠B + 2 ∠1 = 180°
⇒ 2∠1 = 180° – ∠B⇒ ∠1 = 90° – 1 ∠B ........( 1 ) 2
∠B Again, ∠ACB + ∠QCB = 180°⇒ ∠2 = 90° – 1 ∠C ...........( 2 ) 2
In ∆ BOC,
∠1 + ∠2 +∠BOC = 180°⇒ 90° - 1 ∠B + 90° - 1 ∠C + ∠BOC = 180° { ∴ Using ( 1) and ( 2 ) } 2 2 ⇒ ∠BOC = 1 (∠B + ∠C) 2 ⇒ ∠BOC = 1 (180° - ∠A) 2 ⇒ ∠BOC = 90° – 1 ∠A 2 ⇒ 60° = 90° – 1 ∠A 2
∴ ∠A = 60°

