-
In ∆ ABC, draw BE ⊥ AC and CF ⊥ AB and the perpendicular BE and CF intersect at the point O. If ∠ BAC = 70°, then the value of ∠ BOC is
-
- 125°
- 55°
- 150°
- 110°
- 125°
Correct Option: D
As per the given in question , we draw a figure of a triangle ABC and BE ⊥ AC and CF ⊥ AB and the perpendicular BE and CF intersect at the point O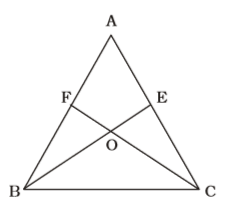
Here , ∠BAC = 70°
∠ABC + ∠ACB = 110° ...(i)
From ∠BCF,
∠CFB + ∠FBC + ∠FCB = 180°
⇒ ∠FBC + ∠FCB = 90° ...(ii)
From ∆ BCE,
∠ECB + ∠EBC = 90° ...(iii)
From (ii) + (iii) – (i) , we get
⇒ ∠EBC + ∠FCB = 180° – 110° = 70°
∴ ∠BOC = 180° – 70° = 110°

