The angle between the external bisectors of two angles of

Home » Aptitude » Plane Geometry » Question

The angle between the external bisectors of two angles of a triangle is 60°. Then the third angle of the triangle is

1. 40°
2. 50°
3. 60°
4. 80°

Correct Option: C

According to question , we draw a figure of a external bisector triangle ABC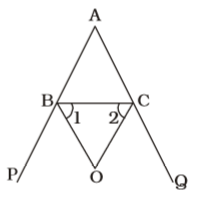

Given , ∠BOC = 60°
∠ABC + ∠CBP = 180°
⇒ ∠B + 2 ∠1 = 180°
⇒ 2∠1 = 180° – ∠B

⇒ ∠1 = 90° –	1	∠B ........( 1 )
	2

∠B Again, ∠ACB + ∠QCB = 180°

⇒ ∠2 = 90° –	1	∠C ...........( 2 )
	2

In ∆ BOC,
∠1 + ∠2 +∠BOC = 180°

⇒ 90° -	1	∠B + 90° -	1	∠C + ∠BOC = 180° { ∴ Using ( 1) and ( 2 ) }
	2		2

⇒ ∠BOC =	1	(∠B + ∠C)
	2

⇒ ∠BOC =	1	(180° - ∠A)
	2

⇒ ∠BOC = 90° –	1	∠A
	2

⇒ 60° = 90° –	1	∠A
	2

∴ ∠A = 60°