Plane Geometry
- In a right angled triangle, the circumcentre of the triangle lies
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure a right angled triangle ,
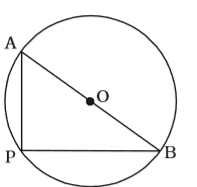
∠APB = 90°Correct Option: C
As per the given in question , we draw a figure a right angled triangle ,

∠APB = 90°
AB = Diameter = hypotenuse of ∆ APB
The angle of a semi-circle is a right angle.
- For a triangle circumcentre lies on one of its sides. The triangleis
l
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of a circle with centre O ,

∠ ABC = 90°Correct Option: A
On the basis of question we draw a figure of a circle with centre O ,

∠ ABC = 90°
∆ ABC is a right angled triangle and ‘O’ is the circumcentre.
- Each of the circles of equal radii with centres A and B pass through the centre of one another circle they cut at C and D then ∠DBC is equal to
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure two circles equal radii with centres A and B ,

In ∆ ABD,
AD = BD = AB = radius
In ∆ ACB,Correct Option: C
As per the given in question , we draw a figure two circles equal radii with centres A and B ,

In ∆ ABD,
AD = BD = AB = radius
In ∆ ACB,
AC = CB = AB = radius
∴ ∠DBC = 60° + 60° = 120°
- The angle subtended by a chord at its centre is 60°, then the ratio between chord and radius is
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of a circle with centre O

OA = OB = r units
∠AOC = 30°; AC = CB
In ∆ AOC,sin AOC = AC OA ⇒ sin 30° = AC r ⇒ 1 = AC 2 r ⇒ AC = r 2 ⇒ AB = 2 × r = r units 2
Correct Option: B
On the basis of question we draw a figure of a circle with centre O

OA = OB = r units
∠AOC = 30°; AC = CB
In ∆ AOC,sin AOC = AC OA ⇒ sin 30° = AC r ⇒ 1 = AC 2 r ⇒ AC = r 2 ⇒ AB = 2 × r = r units 2
∴ Required ratio = 1 : 1
Second Method to solve this question :
OA = OB
∴ ∠OAB = ∠OBA = 60°
∴ ∆ OAB is an equilateral triangle.
∴ OA = OB = AB
- A chord 12 cm long is drawn in a circle of diameter 20 cm. The distance of the chord from the centre is
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of a circle with centre O

Here , diameter = 20 cm ⇒ OC = radius = 10 cm
CD = 12 cm ⇒ CE = ED = 6 cm
∴ OE = √OC² - CE²Correct Option: A
On the basis of question we draw a figure of a circle with centre O

Here , diameter = 20 cm ⇒ OC = radius = 10 cm
CD = 12 cm ⇒ CE = ED = 6 cm
∴ OE = √OC² - CE²
OE = √10² - 6² = √100 - 36
OE = √64 = 8 cm

