426. In ∆ ABC, ∠BAC = 90° and D is the mid–point of BC. Then which of the following relations is true?

1. 1. AD = BD = CD

   
   
   

   2. AD = BD = 2CD
      

   
   
   

   3. AD = 2BD = CD
      

   
   
   

   4. 2AD = BD = CD

   
   
   

---

1. View Hint View Answer Discuss in Forum

   As per the given in question , we draw a figure right-angled triangle BAC
   
   

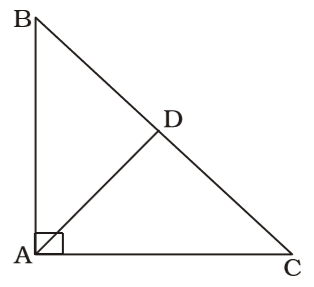
   BD = DC =	1	BC
   	2

   
   ∴AC² = AD² + CD²
   AB² = AD² + BD²
   AC² = AD² + CD²
   On adding, we get
   AB² + AC² = 2AD² + 2CD²
   

   Correct Option: A

   As per the given in question , we draw a figure right-angled triangle BAC
   
   

   BD = DC =	1	BC
   	2

   
   ∴AC² = AD² + CD²
   AB² = AD² + BD²
   AC² = AD² + CD²
   On adding, we get
   AB² + AC² = 2AD² + 2CD²
   ⇒ BC² = 2AD² + 2CD²
   ⇒ 4CD² = 2AD² + 2CD²
   ⇒ AD² = CD²
   ⇒ AD = CD = BD
   Mid point on the hypotenuse of a right angled triangle is equidistant from the vertices.

---

427. If the sides of a triangle are in the ratio 3 : 1	1	: 3	1	then the traigle is
     	4		4

     
     

1. 1. Right triangle
      

   
   
   

   2. Obtuse triangle
      

   
   
   

   3. Equiangular triangle
      

   
   
   

   4. Acute triangle

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Here , Ratio of sides = 3 :	5	:	13
   	4		4

   
   Ratio of sides = 12 : 5 : 13
   

   Correct Option: A

   Here , Ratio of sides = 3 :	5	:	13
   	4		4

   
   Ratio of sides = 12 : 5 : 13
   ∴ 5² + 12² = 13²
   From above relation it is clear that It is a right angled triangle .

---

---

428. The measure of each interior angle of a regular polygon with 8 sides is
     

1. 1. 135°
      

   
   
   

   2. 120°
      

   
   
   

   3. 100°
      

   
   
   

   4. 45°

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Required interior angle =	(2n - 4) × 90°
   	8

   
   Here , n = 8
   

   Required interior angle =	(2 × 8 - 4)	× 90°
   	8

   
   

   Correct Option: A

   Required interior angle =	(2n - 4) × 90°
   	8

   
   Here , n = 8
   

   Required interior angle =	(2 × 8 - 4)	× 90°
   	8

   
   

   Required interior angle =	12 × 90°	= 135°
   	8

---

429. Among the angles 30°, 36°, 45°, 50° one angle cannot be an exterior angle of a regular polygon. The angle is
     

1. 1. 30°
      

   
   
   

   2. 36°
      

   
   
   

   3. 45°
      

   
   
   

   4. 50°

   
   
   

---

1. View Hint View Answer Discuss in Forum

   As we know that Sum of exterior angles of a regular polygon = 360°
   

   But	360°	= 7.2 ≠ a whole number
   	50

   Correct Option: D

   As we know that Sum of exterior angles of a regular polygon = 360°
   

   But	360°	= 7.2 ≠ a whole number
   	50

   
   Hence , 50° angle cannot be an exterior angle of a regular polygon .

---

---

430. If the sum of interior angles of a regular polygon is equal to two times the sum of exterior angles of that polygon, then the number of sides of that polygon is
     

1. 1. 5
      

   
   
   

   2. 6
      

   
   
   

   3. 7
      

   
   
   

   4. 8

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Let Number of sides of regular polygon = n
   Sum of interior angles = (2n – 4) × 90°
   Sum of exterior angles = 360°
   From question ,
   ∴ (2n – 4) × 90° = 2 × 360°
   

   ⇒ 2n - 4 =	2 × 360°	= 8
   	90

   
   ⇒ 2n – 4 = 8
   ⇒ 2n = 8 + 4 = 12
   

   Correct Option: B

   Let Number of sides of regular polygon = n
   Sum of interior angles = (2n – 4) × 90°
   Sum of exterior angles = 360°
   From question ,
   ∴ (2n – 4) × 90° = 2 × 360°
   

   ⇒ 2n - 4 =	2 × 360°	= 8
   	90

   
   ⇒ 2n – 4 = 8
   ⇒ 2n = 8 + 4 = 12
   

   ⇒ n =	12	= 6
   	2

---