Plane Geometry
- If two supplementary angles differ by 44°, then one of the angles is
-
View Hint View Answer Discuss in Forum
Let Supplementary angles = y and 180° – y
According to the question,
Difference between supplementary angles = 44°
⇒ 180° – y – y = 44°
⇒ 180° – 2y = 44°
⇒ 2y = 180° – 44° = 136°Correct Option: A
Let Supplementary angles = y and 180° – y
According to the question,
Difference between supplementary angles = 44°
⇒ 180° – y – y = 44°
⇒ 180° – 2y = 44°
⇒ 2y = 180° – 44° = 136°⇒ y = 136° = 68° 2
- The measure of an angle whose supplement is three times as large as its complement, is
-
View Hint View Answer Discuss in Forum
Let the required angle be y°.
According to the question,
180 – y = 3(90 – y )
⇒ 180 – y = 270 – 3y
⇒ 3y – y = 270 – 180Correct Option: C
Let the required angle be y°.
According to the question,
180 – y = 3(90 – y )
⇒ 180 – y = 270 – 3y
⇒ 3y – y = 270 – 180⇒ 2y = 90 ⇒ y = 90 = 45° 2
- Two poles of height 7 metre and 12 metre stand on a plane ground. If the distance between their feet is 12 metre, the distance between their top will be
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure
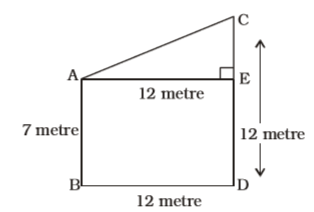
Given that , AB = 7 metre , CD = 12 metre
∴ CE = CD – DE
CE = 12 – 7 = 5 metre
∴ From ∆ AEC,
AC = √AE² + EC²Correct Option: B
As per the given in question , we draw a figure

Given that , AB = 7 metre , CD = 12 metre
∴ CE = CD – DE
CE = 12 – 7 = 5 metre
∴ From ∆ AEC,
AC = √AE² + EC²
AC = √12² + 5² = √144 + 25
AC = √169 = 13 metre
- A tree of height ‘h’ metres is broken by a storm in such a way that its top touches the ground at a distance of ‘x’ metres from its root. Find the height at which the tree is broken. (Here h > x)
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure
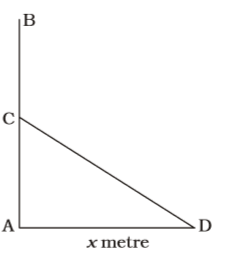
AB = Height of tree = h metre , AC = Required height = y metre
BC = CD = Broken part of tree = (h – y) metre
∴ In ∆ ACD,
AC² + AD² = CD²
⇒ y² + x² = (h – y)²
⇒ y² + x² = h² + y² – 2hy
⇒ x² = h² – 2hyCorrect Option: B
According to question , we draw a figure

AB = Height of tree = h metre , AC = Required height = y metre
BC = CD = Broken part of tree = (h – y) metre
∴ In ∆ ACD,
AC² + AD² = CD²
⇒ y² + x² = (h – y)²
⇒ y² + x² = h² + y² – 2hy
⇒ x² = h² – 2hy
⇒ 2hy = h² – x²⇒ y = h² - x² metre 2h
- If the angles of a triangle ABC are in the ratio 2 : 3 : 1, then the angles ∠A,∠B and ∠C are
-
View Hint View Answer Discuss in Forum
Here , Ratio = 2 : 3 : 1
Let the angles of a triangle are 2y , 3y and y .
We know that Sum of three angles of triangle = 180°
∠ A = 2y°
∠ B = 3y°
∠ C = y°
⇒ 2y° + 3y ° + y° = 180°
⇒ 6 y° = 180°⇒ y = 180 = 30 6
Correct Option: A
Here , Ratio = 2 : 3 : 1
Let the angles of a triangle are 2y , 3y and y .
We know that Sum of three angles of triangle = 180°
∠ A = 2y°
∠ B = 3y°
∠ C = y°
⇒ 2y° + 3y ° + y° = 180°
⇒ 6 y° = 180°⇒ y = 180 = 30 6
∴ ∠ A = 2y = 2 × 30° = 60°
∠ B = 3y = 3 × 30 = 90°
∠ C = y = 30°

