Plane Geometry
- A square is inscribed in a quarter-circle in such a manner that two of its adjacent vertices lie on the two radii at an equal distance from the centre, while the other two vertices lie on the circular arc. If the square has sides of length x, then the radius of the circle is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure a square inscribed in a quarter-circle ,
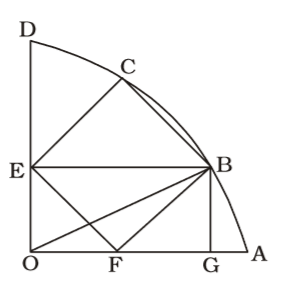
OE = OF
EF = x units
∴ From ∆ OEF,
2OE² = EF²
⇒ √2 × OE = EF = x⇒ OE = x √2
BE = diagonal of square EFBC = √2 x
∴ OB = √OE² + EB²OB = √ 
x 
² + (√2x)² √2 OB = √ x² + 2x² 2 OB = √ x² + 4x² 2
Correct Option: D
As per the given in question , we draw a figure a square inscribed in a quarter-circle ,

OE = OF
EF = x units
∴ From ∆ OEF,
2OE² = EF²
⇒ √2 × OE = EF = x⇒ OE = x √2
BE = diagonal of square EFBC = √2 x
∴ OB = √OE² + EB²OB = √ 
x 
² + (√2x)² √2 OB = √ x² + 2x² 2 OB = √ x² + 4x² 2 OB = √ 5x² 2 OB = √5x units √2
- Each interior angle of a regular polygon is three times its exterior angle, then the number of sides of the regular polygon is :
-
View Hint View Answer Discuss in Forum
As per the given question ,
If the number of sides of regular polygon be n, then(2n - 4) 90° = 360° × 3 n n
Correct Option: B
As per the given question ,
If the number of sides of regular polygon be n, then(2n - 4) 90° = 360° × 3 n n
⇒ 2n – 4 = 4 × 3
⇒ 2n = 12 + 4 = 16
∴ n = 8
- The difference between the exterior and interior angles at a vertex of a regular polygon is 150°. The number of sides of the polygon is
-
View Hint View Answer Discuss in Forum
Let the number of sides of polygon be n. Then
According to question ,
Difference = Interior angle of a polygon - Exterior angle of a polygon = 150∴ (2n - 4) × 90° - 360° = 150 n n ⇒ (2n - 4) × 3 - 12 = 5 n n
Correct Option: C
Let the number of sides of polygon be n. Then
According to question ,
Difference = Interior angle of a polygon - Exterior angle of a polygon = 150∴ (2n - 4) × 90° - 360° = 150 n n ⇒ (2n - 4) × 3 - 12 = 5 n n ⇒ 6n - 12 - 12 = 5 n
⇒ 6n – 24 = 5n
⇒ n = 24
- The number of sides in two regular polygons are in the ratio 5 : 4 and the difference between each interior angle of the polygons is 6°. Then the number of sides are
-
View Hint View Answer Discuss in Forum
The ratio of number of sides in two regular polygons = 5 : 4
Let the number of sides be 5k and 4k respectively.
Difference between each interior angle of the polygons = 6°⇒ (2 × 5k - 4)90° - (2 × 4k - 4) × 90° = 6° 5n 4n
Correct Option: A
The ratio of number of sides in two regular polygons = 5 : 4
Let the number of sides be 5k and 4k respectively.
Difference between each interior angle of the polygons = 6°⇒ (2 × 5k - 4)90° - (2 × 4k - 4) × 90° = 6° 5n 4n 
∴ Each interior angle = 
2n - 4 
× 90° 
n
⇒ (10k – 4) × 360° – (8k – 4) × 450° = 20k × 6°
⇒ (10k – 4) × 12 – (8k – 4)15 = 4k
⇒ 120k – 48 – 120k + 60 = 4k
⇒ 4k = 12 ⇒ k = 3
∴ Number of sides = 15 and 12
- Each internal angle of regular polygon is two times its external angle. Then the number of sides of the polygon is :
-
View Hint View Answer Discuss in Forum
According to question ,
Each internal angle of regular polygon is two times its external angle .
Let the number of sides of regular polygon be n.∴ 
2n - 4 
× 90° = 2 × 360° n n
Correct Option: B
According to question ,
Each internal angle of regular polygon is two times its external angle .
Let the number of sides of regular polygon be n.∴ 
2n - 4 
× 90° = 2 × 360° n n
⇒ (2n – 4) = 8
⇒ 2n = 12
⇒ n = 6

