A square is inscribed in a quarter-circle in such a manner

Home » Aptitude » Plane Geometry » Question

A square is inscribed in a quarter-circle in such a manner that two of its adjacent vertices lie on the two radii at an equal distance from the centre, while the other two vertices lie on the circular arc. If the square has sides of length x, then the radius of the circle is

1. √2x
2. 16x
  π + 4
3. 2x
  √π
4. √5x
  √2

Correct Option: D

As per the given in question , we draw a figure a square inscribed in a quarter-circle ,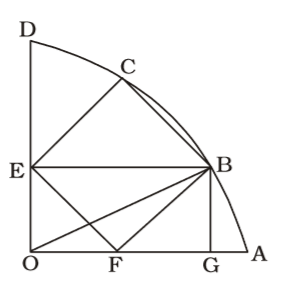

OE = OF
EF = x units
∴ From ∆ OEF,
2OE² = EF²
⇒ √2 × OE = EF = x

⇒ OE =	x
	√2

BE = diagonal of square EFBC = √2 x
∴ OB = √OE² + EB²

OB = √		x		²	+ (√2x)²
		√2

OB = √	x²	+ 2x²
	2

OB = √	x² + 4x²
	2

OB = √	5x²
	2

OB =	√5x	units
	√2