Plane Geometry
- A square ABCD is inscribed in a circle of unit radius. Semicircles are described on each side as a diameter. The area of the region bounded by the four semicircles and the circle is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure square ABCD in which is inscribed in a circle of unit radius ,
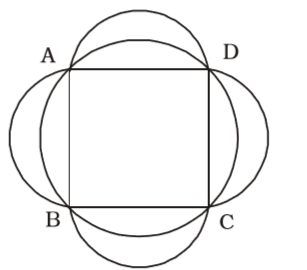
BD = 2 units
AB = √2 units
Area of square = 2 square unitsArea of four semicircles = 4 × πr² 2
Correct Option: B
As per the given in question , we draw a figure square ABCD in which is inscribed in a circle of unit radius ,

BD = 2 units
AB = √2 units
Area of square = 2 square unitsArea of four semicircles = 4 × πr² 2 Area of four semicircles = 4 × π × 1/2 2
Area of four semicircles = πsq. units
∴ Required area = 2 + π – π = 2 sq. units.
- In a circle of radius 17 cm, two parallel chords of length 30 cm and 16 cm are drawn. If both the chords are on the same side of the centre, then the distance between the chords is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure circle with centre O

From figure , AE = 15 cm [∵AB = 30 cm]
OA = 17 cm
∴ OE = √17² - 15²
OE = √(17 + 15)(17 - 15)
OE = √32 × 2 = 8 cm
Again, CF = 8 cm
OC = 17 cm
∴ OF = √17² - 8²
OF = √(17 + 8)(17 - 8)Correct Option: B
As per the given in question , we draw a figure circle with centre O

From figure , AE = 15 cm [∵AB = 30 cm]
OA = 17 cm
∴ OE = √17² - 15²
OE = √(17 + 15)(17 - 15)
OE = √32 × 2 = 8 cm
Again, CF = 8 cm
OC = 17 cm
∴ OF = √17² - 8²
OF = √(17 + 8)(17 - 8)
OF = √25 × 9 = 15 cm
∴ Distance between chords = EF = OF - CF = 15 – 8 = 7 cm
- AB is the chord of a circle with centre O and DOC is a line segment originating from a point D on the circle and intersecting AB produced at C such that BC = OD. If ∠BCD = 20°, then ∠AOD=?
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of a circle with centre O and AB is the chord ,

Given , BC = DO = OA
∠DAB = 90°Correct Option: C
On the basis of question we draw a figure of a circle with centre O and AB is the chord ,

Given , BC = DO = OA
∠DAB = 90°
∠DOA = 2 × ∠DCA
or 2 ∠BCD = 40°
- Two circles of same radius 5 cm, intersect each other at A and B. If AB = 8 cm, then the distance between the centre is :
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of two circles with centres O and O' ,

Here , AC = 4 cm
OA = 5 cmCorrect Option: A
On the basis of question we draw a figure of two circles with centres O and O' ,

Here , AC = 4 cm
OA = 5 cm
OC = √5² - 4² = 3 cm
OƠ = 2OC = 2 × 3 = 6 cm
- Two circles with centre P and Q intersect at B and C. A, D are points on the circle such that A, C, D are collinear. If ∠APB = 130°, and ∠BQD = x°, then the value of x is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure two circles with centre P and Q intersect at B and C ,

Given that , ∠APB = 130°, and ∠BQD = x°,∴ ∠ BCA = 130° = 65° 2
⇒ ∠BCD = 180° – 65° = 115°
Correct Option: B
As per the given in question , we draw a figure two circles with centre P and Q intersect at B and C ,

Given that , ∠APB = 130°, and ∠BQD = x°,∴ ∠ BCA = 130° = 65° 2
⇒ ∠BCD = 180° – 65° = 115°
⇒ Ext. ∠BQD = 2 × 115° = 230°
∴ ∠BQD = 360° – 230° = 130°

