Plane Geometry
- The measure of the angle between the internal and external bisectors of an angle is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of triangle ABC

From figure ,∠ACF = ∠FCB = ∠C 2 ∠ACE = ∠ECD = 180° - ∠C 2 ∠ACE = 90° - ∠C 2
∴ ∠FCE = ∠FCA + ∠ACE
Correct Option: D
As per the given in question , we draw a figure of triangle ABC

From figure ,∠ACF = ∠FCB = ∠C 2 ∠ACE = ∠ECD = 180° - ∠C 2 ∠ACE = 90° - ∠C 2
∴ ∠FCE = ∠FCA + ∠ACE∠FCE = ∠C + 90° - ∠C = 90° 2 2
- The sum of three altitudes of a triangle is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of triangle ABC

AP < AB
BQ < BC
CR < ACCorrect Option: B
As per the given in question , we draw a figure of triangle ABC

AP < AB
BQ < BC
CR < AC
∴ AP + BQ + CR < AB + BC + AC
⇒The sum of three altitudes of a triangle is less than the sum of sides.
- ∆ABC is an isosceles right angled triangle having ∠ C = 90°. If D is any point on AB, then AD2 + BD2 is equal to
-
View Hint View Answer Discuss in Forum
We draw a figure of an isosceles right angled triangle having ∠ C = 90° ,
AC² + CB² = AB²
⇒ 2BC² = (AD + DB)²
⇒ 2BC² = AD² + DB² + 2AD.BD ..... (i)
∆ CEB and ∆CED are right angles.
CD² = CE² + ED²
and, BC² = CE² + BE²
BC² – CD² = BE² – DE²
BC² – CD² = (BE + DE) (BE – DE)
BC² – CD² = (AE + DE) (BE – DE)Correct Option: B
We draw a figure of an isosceles right angled triangle having ∠ C = 90° ,

AC² + CB² = AB²
⇒ 2BC² = (AD + DB)²
⇒ 2BC² = AD² + DB² + 2AD.BD ..... (i)
∆ CEB and ∆CED are right angles.
CD² = CE² + ED²
and, BC² = CE² + BE²
BC² – CD² = BE² – DE²
BC² – CD² = (BE + DE) (BE – DE)
BC² – CD² = (AE + DE) (BE – DE)
BC² – CD² = AD . BD ..... (ii)
∴ From equations (i) and (ii)
AD² + DB² = 2CD²
- ∆ABC is isosceles having AB = AC and ∠A = 40°. Bisectors PO and OQ of the exterior angles ∠ABD and &Ang;ACE formed by producing BC on both sides, meet at O. Then the value of ∠BOC is
-
View Hint View Answer Discuss in Forum
On the basis of given in question , we draw a figure of an isosceles triangle ABC which bisectors PO and OQ of the exterior angles ∠ABD and &Ang;ACE formed by producing BC on both sides, meet at O
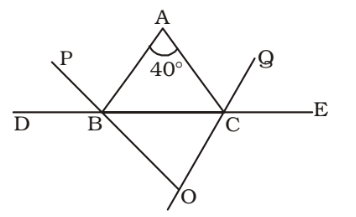
Given , AB = AC
∴ ∠ABC = ∠ACB = 140 ÷ 2 = 70°
∴ ∠ABD = ∠ACE = 180° - 70° = 110°Correct Option: A
On the basis of given in question , we draw a figure of an isosceles triangle ABC which bisectors PO and OQ of the exterior angles ∠ABD and &Ang;ACE formed by producing BC on both sides, meet at O

Given , AB = AC
∴ ∠ABC = ∠ACB = 140 ÷ 2 = 70°
∴ ∠ABD = ∠ACE = 180° - 70° = 110°
∴ ∠PBD = 55° = ∠CBO
∠QCE = ∠BCO = 55°
&there4 ∠BOC = 180° – 2 × 55° = 180° – 110° = 70°
- The vertical angle A of an isosceles triangle ∆ABC is three times the angle B of it. The measure of the angle A is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of an isosceles triangle ABC
In ∆ABC,
AB = AC
∴ ∠B = ∠C
∵ ∠A + ∠B + ∠C = 180°∴ ∠A + ∠A + ∠A = 180° 3 3 ⇒ 3∠A + ∠A + ∠A = 180° 3 ⇒ 5∠A = 180° 3
Correct Option: B
As per the given in question , we draw a figure of an isosceles triangle ABC

In ∆ABC,
AB = AC
∴ ∠B = ∠C
∵ ∠A + ∠B + ∠C = 180°∴ ∠A + ∠A + ∠A = 180° 3 3 ⇒ 3∠A + ∠A + ∠A = 180° 3 ⇒ 5∠A = 180° 3 ⇒ ∠A = 180° × 3 = 108° 5

