Correct Option: B

We draw a figure of an isosceles right angled triangle having ∠ C = 90° ,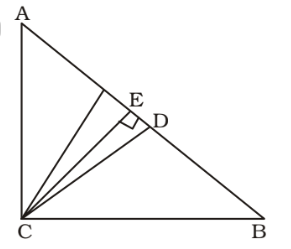

AC² + CB² = AB²
⇒ 2BC² = (AD + DB)²
⇒ 2BC² = AD² + DB² + 2AD.BD ..... (i)
∆ CEB and ∆CED are right angles.
CD² = CE² + ED²
and, BC² = CE² + BE²
BC² – CD² = BE² – DE²
BC² – CD² = (BE + DE) (BE – DE)
BC² – CD² = (AE + DE) (BE – DE)
BC² – CD² = AD . BD ..... (ii)
∴ From equations (i) and (ii)
AD² + DB² = 2CD²