-
In ∆ ABC, ∠BAC = 90° and D is the mid–point of BC. Then which of the following relations is true?
-
- AD = BD = CD
- AD = BD = 2CD
- AD = 2BD = CD
- 2AD = BD = CD
Correct Option: A
As per the given in question , we draw a figure right-angled triangle BAC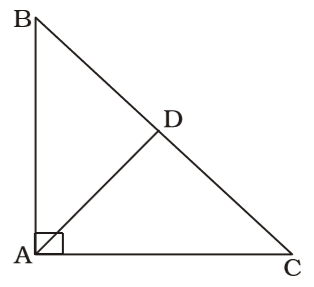
| BD = DC = | BC | |
| 2 |
∴AC² = AD² + CD²
AB² = AD² + BD²
AC² = AD² + CD²
On adding, we get
AB² + AC² = 2AD² + 2CD²
⇒ BC² = 2AD² + 2CD²
⇒ 4CD² = 2AD² + 2CD²
⇒ AD² = CD²
⇒ AD = CD = BD
Mid point on the hypotenuse of a right angled triangle is equidistant from the vertices.

