-
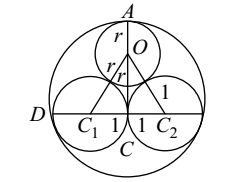
Two circles of unit radius touch each other and each of them touches internally a circle of radius two, as shown in the following figure. The radius of the circle which thouches all the three circles:
-
- 5
-
3 2 -
2 3 -
2 5 - None of these
Correct Option: C
From given figure , we can see that
CC1 = 1, OC1 = 1 + r
OC = AC – AO = CD – AO = 2 – r [ AC and CD are the radii of the bigger circle ]
∴ (OC1)2 = (CC1)2 + (OC)2
⇒ (1 + r)2 = 12 + (2 - r)2
⇒ 1 + r2 + 2r = 1 + 4 + r2 - 4r ⇒ 2r + 4r = 4 ⇒ 6r = 4
| ⇒ r = | 2 |
| 3 |