-
Two chords AB and CD of a circle with centre O intersect each other at the point P. If ∠AOD = 20° and ∠BOC = 30°, then ∠BPC is equal to:
-
- 50°
- 20°
- 25°
- 30°
- 50°
Correct Option: C
On the basis of question we draw a figure of a circle with centre in which two chords AB and CD intersect each other at the point P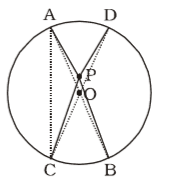
Given that , ∠AOD = 20° and ∠BOC = 30°
∠BOC = 2 ∠BAC
∠AOD = 2 ∠DCA
∴ ∠BOC + ∠AOD = 2 (∠BAC + ∠DCA)
∠BOC + ∠AOD = 2 ∠BPC (Exterior angles' sum)
∴ 2∠BPC = 20° + 30° = 50°
⇒ ∠BPC = 25°

