-
AB and CD are two parallel chords of a circle lying on the opposite side of the centre and the distance between them is 17 cm. The length of AB and CD are 10 cm and 24 cm respectively. The radius (in cm) of the circle is :
-
- 13
- 9
- 18
- 15
- 13
Correct Option: A
According to question , we draw a figure of a circle with centre O , 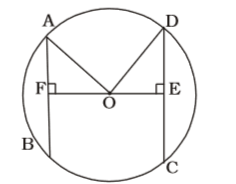
AB = 10 cm.
∴ AF = FB = 5 cm.
CD = 24 cm.
∴ CE = DE = 12 cm.
Let OE = y cm
∴ OF = (17 – y) cm
From ∆ ODE,
OD = √OE² + DE²
OD = √y² + 12² ..... (i)
From ∆ OAF,
OA = √OF² + AF²
OA = √(17 - y)² + 5² ..... (ii)
∵ OA = OD
∴ √y² + 12² = √(17 - y)² + 5²
⇒ y² + 144 = 289 – 34y + y² + 25
⇒ 34y = 289 + 25 – 144 = 170
| ⇒ y = | = 5 | |
| 34 |
∴ From equation (i),
OD = √y² + 12² = √5² + 144
OD = √169 = 13 cm.

