If O is the circumcentre of a triangle ABC lying inside

Home » Aptitude » Plane Geometry » Question

If O is the circumcentre of a triangle ABC lying inside the triangle, then ∠OBC + ∠BAC is equal to

1. 90°
2. 60°
3. 110°
4. 120°

Correct Option: A

As per the given in question , we draw a figure of a triangle ABC and O is the circumcentre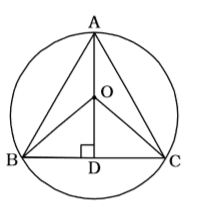

In ∆ OBC ∵ OB = OC
∴ ∠ OBC = ∠OCB
∴ ∠ BOC = 180° – 2 ∠OBC
In ∆ OBD,
∠OBD = ∠ OBC = 90° – ∠BOD
Angle subtended by an arc at the centre is twice to that subtended at the circumference.

∴ ∠BAC =	1	∠OBC
	2

∠BAC =	1	(180° - 2∠OBC
	2

∠BAC = 90° - ∠OBC
∴ ∠BAC + ∠OBC = 90°