-
In a circle with centre O, AB is a diameter and CD is a chord which is equal to the radius OC. AC and BD are extended in such a way that they intersect each other at a point P, exterior to the circle. The measure of ∠APB is
-
- 30°
- 45°
- 60°
- 90°
- 30°
Correct Option: C
As per the given in question , we draw a figure of a circle with centre O, 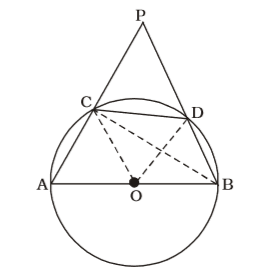
In ∆ OCD,
OC = OD = CD = radius
∴ ∆ OCD is an equilateral triangle.
∴ ∠COD = 60°
| ∠CBD = | ∠COD = 30° | |
| 2 |
∠ACB is an angle of semi-circle.
∴ ∠ACB = 90°
∴ ∠BCP = 180° – ∠ACB
∠BCP = 180° – 90° = 90°
In ∆ BCP, ∠BCP = 90°,∠CBP = ∠CBD = 30°
∴ ∠BCP + ∠CBP + ∠CPB = 180°
⇒ 90° + 30° + ∠CPB = 180°
⇒ ∠CPB = 60° = ∠APB

