-
BL and CM are medians of DABC right-angled at A and BC = 5 cm. If BL = 3√5/2 cm, then the length of CM is
-
- 2√5cm
- 5√2cm
- 10√2cm
- 4√5cm
Correct Option: A
According to question , we draw a figure right-angled triangle BAC 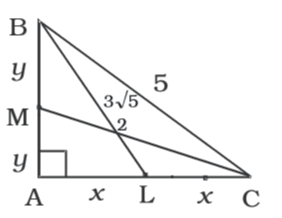
Since BL is the Median AL = LC = x (say). Since CM is the Median, BM = MA = y (say)
AB² + AC² = 25 ...(i)
| ⇒ |  |  | ² | = (2y)² + x² | |
| 2 |
| ⇒ | = 4y² + x² | |
| 4 |
| ⇒ 4y² = | - x² ...(ii) | |
| 4 |
In ∆ ABC, BC² = AB² + AC²
⇒ 25 = (2y)² + (2x)²
25 = 4y² + 4x²
| ⇒ 25 = | - x² + 4y² | |
| 4 |
| 3x² = | ⇒ x² = | ||
| 4 | 12 |
| Put in (ii) ⇒ 4y² = | - | ||
| 4 | 12 |
| ⇒ 4y² = | |
| 12 |
| ⇒ 4y² = | ⇒ y² = | = | |||
| 12 | 12 × 4 | 3 |
Now , CM = √y² + 4x²
| CM = | √ | + 4 |  |  | ||
| 3 | 12 |
| CM = | √ | + | ||
| 3 | 3 |
| CM = | √ | |
| 3 |
CM = √20 = 2 √5cm.

