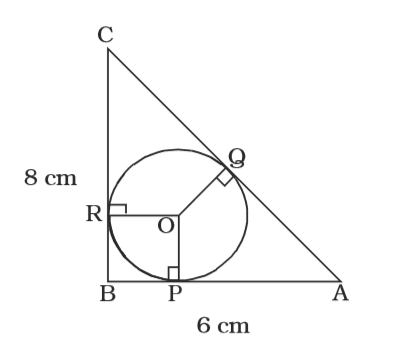
∆ ABC is a right angled triangle with AB = 6 cm, BC

Home » Aptitude » Plane Geometry » Question

∆ ABC is a right angled triangle with AB = 6 cm, BC = 8 cm. O is the incentre of the triangle. The radius of the in-circle is :

1. 3 cm
2. 4 cm
3. 2 cm
4. 5 cm

Correct Option: C

As per the given in question , we draw a figure of a right angled triangle ABC and O is the incentre of the triangle

Given , AB = 6 cm, BC = 8 cm
OP = OQ = OR = r (let)
∠CBA = 90°
From ∆ABC ,
∴ AC = √AB² + BC²
AC = √6² + 8² = √36 + 64
AC = √100 = 10 cm.
Area of ∆ ABC = Area of ( ∆ AOC + ∆ BOC + ∆ AOB)

⇒	1	× 6 × 8 =	1	× AC × OQ +	1	× BC × OR +	1	× AB × OP
	2		2		2		2

⇒ 24 =	1	× 10 × r +	1	× 8 × r +	1	× 6 × r
	2		2		2

⇒ 24 = 5r + 4r + 3r

⇒ 12r = 24 ⇒ r =	24	= 2 cm.
	2