-
The circumcentre of a triangle ABC is O. If ∠BAC = 85°, ∠BCA = 75°, then ∠OAC is of
-
- 70°
- 72°
- 75°
- 74°
- 70°
Correct Option: A
On the basis of question we draw a figure of a a triangle ABC whose circumcentre is O , 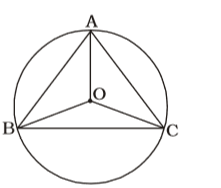
Point ‘O’ is equidistant from the vertices of triangle ABC.
∴ OA = OB = OC
∴ ∠OAC = ∠OCA, ∠OBC = ∠OCB; ∠OAB = ∠OBA
∴ In ∆ ABC,
∠ABC = 180° – 85° – 75° = 20°
∴ ∠AOC = 2 ∠ABC = 2 × 20° = 40°
∴ In ∆ AOC,
2 ∠OAC + 40° = 180°
⇒ 2 ∠OAC = 180° – 40° = 140°
| ⇒ ∠OAC = | = 70° | |
| 2 |

