116. 150 workers were engaged to finish a piece of work in a certain number of days. Four workers dropped on the second day, four more workers dropped on third day and so on. It takes 8 more days to finish the work now. Find the number of days in which the work was completed?

1. 1. 28

   
   
   

   2. 24

   
   
   

   3. 25

   
   
   

   4. 30

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Let 150 workers complete the work in x days.
   ∴ 150 × x = 150 + 146 + .... to
   (x + 8) terms
   On putting x = 17
   LHS = 150 × 17 = 2550
   RHS = 150 + 146 + .... to 25 terms
   a = 150, d = –4, n = 25
   

   ∴ S =	n	[2a + (n–1) d]
   	2

   
   

   =	25	[2 × 150 + 24 × (–4)]
   	2

   
   

   =	25	(300 – 96) =	25 × 204	= 2550
   	2		2

   
   Note : It is better to solve by options.

   Correct Option: C

   Let 150 workers complete the work in x days.
   ∴ 150 × x = 150 + 146 + .... to
   (x + 8) terms
   On putting x = 17
   LHS = 150 × 17 = 2550
   RHS = 150 + 146 + .... to 25 terms
   a = 150, d = –4, n = 25
   

   ∴ S =	n	[2a + (n–1) d]
   	2

   
   

   =	25	[2 × 150 + 24 × (–4)]
   	2

   
   

   =	25	(300 – 96) =	25 × 204	= 2550
   	2		2

   
   Note : It is better to solve by options.

---

117. 12 men and 18 boys working
     

     7	1
     	2

     
     hours a day can do a work in 60 days. If one man works equal to 2 boys, then the number of boys required to help 21 men to do twice the work in 50 days working 9 hours a day will be :

1. 1. 42

   
   
   

   2. 44

   
   
   

   3. 46

   
   
   

   4. None of these

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Using Rule 1,
   12 men + 18 boys = 21 men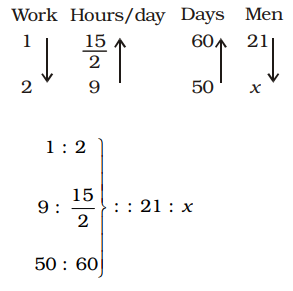
   
   

   ⇒ 9 × 50 × x =	15	× 60 × 21 × 2
   	2

   
   

   ⇒ x =	15 × 60 × 21 × 2	= 42
   	2 × 9 × 50 ×

   
   ∴ Number of boys
   = 2 × 21 = 42

   Correct Option: A

   Using Rule 1,
   12 men + 18 boys = 21 men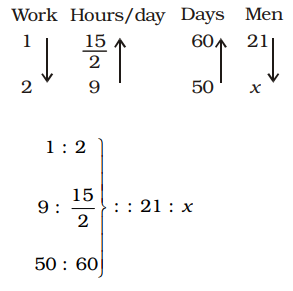
   
   

   ⇒ 9 × 50 × x =	15	× 60 × 21 × 2
   	2

   
   

   ⇒ x =	15 × 60 × 21 × 2	= 42
   	2 × 9 × 50 ×

   
   ∴ Number of boys
   = 2 × 21 = 42

---

---

118. 8 workers can build a wall 18 m long, 2 m broad and 12 m high in 10 days, working 9 hours a day. Find how many workers will be able to build a wall 32 m long, 3 m broad and 9 m high in 8 days working 6 hours a day ?

1. 1. 16

   
   
   

   2. 20

   
   
   

   3. 30

   
   
   

   4. 10

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Using Rule 1,
   
   ⇒ 18 × 2 × 12 × 6 × 8x = 32 × 3 × 9 × 9 × 10 × 8
   

   ⇒ x =	32 × 3 × 9 × 9 × 10 × 8	= 30 days
   	18 × 2 × 12 × 6 × 8

   Correct Option: C

   Using Rule 1,
   
   ⇒ 18 × 2 × 12 × 6 × 8x = 32 × 3 × 9 × 9 × 10 × 8
   

   ⇒ x =	32 × 3 × 9 × 9 × 10 × 8	= 30 days
   	18 × 2 × 12 × 6 × 8

---

119. If 12 carpenters working 6 hours a day can make 460 chairs in 240 days, then the number of chairs made by 18 carpenters in 36 days each working 8 hours a day is

1. 1. 92

   
   
   

   2. 132

   
   
   

   3. 138

   
   
   

   4. 126

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Using Rule 1,
   
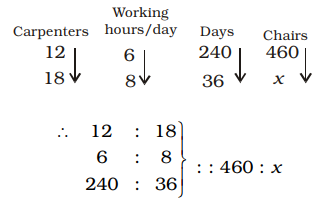
   ⇒ 12 × 6 × 240 × x
   ⇒ = 18 × 8 × 36 × 460
   

   ⇒ x =	18 × 8 × 36 × 460	= 138
   	12 × 6 × 240

   Correct Option: C

   Using Rule 1,
   
   ⇒ 12 × 6 × 240 × x
   ⇒ = 18 × 8 × 36 × 460
   

   ⇒ x =	18 × 8 × 36 × 460	= 138
   	12 × 6 × 240

---

---

120. A farmer can plough a field working 6 hours per day in 18 days. The worker has to work how many hours per day to finish the same work in 12 days ?

1. 1. 7 hrs

   
   
   

   2. 9 hrs

   
   
   

   3. 11 hrs

   
   
   

   4. 13 hrs

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Using Rule 1,
   D₁T₁ = D₂T₂
   ⇒ 18 × 6 = 12 × T₂
   

   ⇒ T2 =	18 × 6	= 9 hours
   	12

   Correct Option: B

   Using Rule 1,
   D₁T₁ = D₂T₂
   ⇒ 18 × 6 = 12 × T₂
   

   ⇒ T2 =	18 × 6	= 9 hours
   	12

---