Number System
- If the sum of the digits of any number, lying between 100 and 1000 is subtracted from the
number, then the difference is always divisible by
-
View Hint View Answer Discuss in Forum
Any number between 100 and 1000 may be written as 100m + 10n + K where 0 < m <
9, 0 < n < 9 and 0 < K < 9.
∴ (100m + 10n + K) – (m + n + K) = 99m + 9n = 9 (11m + n) = multiplie of 9.
Hence divisible by 9.Correct Option: B
Any number between 100 and 1000 may be written as 100m + 10n + K where 0 < m <
9, 0 < n < 9 and 0 < K < 9.
∴ (100m + 10n + K) – (m + n + K) = 99m + 9n = 9 (11m + n) = multiplie of 9.
Hence divisible by 9.
- A certain number on being divided successively by 9, 11 and 13 leaves remainder 8, 9 and 8 respectively. What are the remainders when the same number be divided by reversing the order of divisors?
-
View Hint View Answer Discuss in Forum
We proceed to find the number that is least as mentioned below.
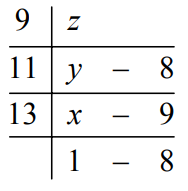
x = 13 × 1 + 8 = 21
y = 11x + 9 = 11 × 21 + 9 = 231 + 9 = 240
z = 9y + 8 = 9 × 240 = 8 = 2160 + 8 = 2168.
Now, divide 2168 by 13, 11 and 9.
Hence, the remainders are 10, 1 and 6 respectively.
Remark : To determine the least number, we have taken the last quotient as 1.Correct Option: A
We proceed to find the number that is least as mentioned below.
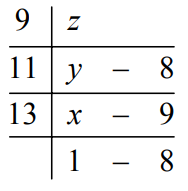
x = 13 × 1 + 8 = 21
y = 11x + 9 = 11 × 21 + 9 = 231 + 9 = 240
z = 9y + 8 = 9 × 240 = 8 = 2160 + 8 = 2168.
Now, divide 2168 by 13, 11 and 9.
Hence, the remainders are 10, 1 and 6 respectively.
Remark : To determine the least number, we have taken the last quotient as 1.
- A certain number when successively divided by 8 and 11 leaves remainder 3 and 7
respectively. Find the remainder if the same number is divided by 88.
-
View Hint View Answer Discuss in Forum
It is to be noted that 88= 8 × 11
Here, d1 = 8, d2 = 11, r1 = 3, r2 = 7.
Where d1, d2 are divisors and r1 and r2 are respective remainders.
∴ Required remainder = d1r2 + r1
= 8 × 7 + 3 = 56 + 3 = 59Correct Option: C
It is to be noted that 88= 8 × 11
Here, d1 = 8, d2 = 11, r1 = 3, r2 = 7.
Where d1, d2 are divisors and r1 and r2 are respective remainders.
∴ Required remainder = d1r2 + r1
= 8 × 7 + 3 = 56 + 3 = 59
- Find the number of prime factors in the product of 2512 × 107 × 147.
-
View Hint View Answer Discuss in Forum
We break each base number into prime factors.
Now, 2512
= (5 × 5)12 = 512 × 512
107 = (2 × 5)7 = 27 × 57
and , 147 = (2 × 7)7 = 27 × 77
∴ 2512 × 107 × 147 = 512 × 512 × 27 × 57 × 27 × 77
= 512 + 12 + 7 × 27 + 7 × 77 = 531 × 214 × 77
∴ Number of prime factors = 31 + 14 + 7 = 52Correct Option: B
We break each base number into prime factors.
Now, 2512
= (5 × 5)12 = 512 × 512
107 = (2 × 5)7 = 27 × 57
and , 147 = (2 × 7)7 = 27 × 77
∴ 2512 × 107 × 147 = 512 × 512 × 27 × 57 × 27 × 77
= 512 + 12 + 7 × 27 + 7 × 77 = 531 × 214 × 77
∴ Number of prime factors = 31 + 14 + 7 = 52
- Find the number of prime factors in 307 × 225 × 3412 × 125.
-
View Hint View Answer Discuss in Forum
We break each base number into prime factors.
Now, 307= (2 × 3 × 5)7= 27 × 37 × 57
225 = (2 × 11)5 = 25 × 115
3412 = (2 × 17)12 = 212 × 1712
125 = (3 × 2 × 2)5 = 35 × 25 × 25
∴ 307 × 22 × 3412 × 125 = 27 × 37 × 57 × 25 × 115 × 212 × 1712 × 35 × 25 × 25
= 27+5+12+5+5 × 37+5 × 57 × 115 × 1712
= 234 × 312 × 57 × 115 × 1712
∴ The required number of prime factors
= 34 + 12 + 7 + 5 + 12 = 70Correct Option: A
We break each base number into prime factors.
Now, 307= (2 × 3 × 5)7= 27 × 37 × 57
225 = (2 × 11)5 = 25 × 115
3412 = (2 × 17)12 = 212 × 1712
125 = (3 × 2 × 2)5 = 35 × 25 × 25
∴ 307 × 22 × 3412 × 125 = 27 × 37 × 57 × 25 × 115 × 212 × 1712 × 35 × 25 × 25
= 27+5+12+5+5 × 37+5 × 57 × 115 × 1712
= 234 × 312 × 57 × 115 × 1712
∴ The required number of prime factors
= 34 + 12 + 7 + 5 + 12 = 70

