Number System
- Find the largest number, which exactly divides every number of the form (n3 – n) (n –2) where n isa natural number greater than 2.
-
View Hint View Answer Discuss in Forum
(n3 – n) (n – 2)
= n (n – 1) (n + 1) (n – 2)Correct Option: C
(n3 – n) (n – 2)
= n (n – 1) (n + 1) (n – 2)
When n = 3,
Number = 3 × 2 × 4 = 24
- How many numbers between 1000 and 5000 are exactly divisible by 225 ?
-
View Hint View Answer Discuss in Forum
When we divide 1000 by 225,
quotient = 4
When we divide 5000 by 225,
quotient = 22Correct Option: B
When we divide 1000 by 225,
quotient = 4
When we divide 5000 by 225,
quotient = 22
∴ Required answer = 22 – 4 = 18
- The greatest whole number, by which the expression n4 + 6n3 +11n2 + 6n + 24 is divisible for every natural number n, is
-
View Hint View Answer Discuss in Forum
For n = 1
n4 + 6n3 +11n2 + 6n + 24
⇒ n4 + 6n3 +11n2 + 6n + 24 = 1 + 6 + 11 + 6 + 24 = 48
For n = 2
n4 + 6n3 +11n2 + 6n + 24Correct Option: D
For n = 1
n4 + 6n3 +11n2 + 6n + 24
⇒ n4 + 6n3 +11n2 + 6n + 24 = 1 + 6 + 11 + 6 + 24 = 48
For n = 2
n4 + 6n3 +11n2 + 6n + 24 = 16 + 48 + 44 + 12 + 24
⇒ n4 + 6n3 +11n2 + 6n + 24 = 144 , which is divisible by 48.
Clearly, 48 is the required number.
- It is given that (232 + 1) is exactly divisible by a certain number. which one of the following is also definitely divisible by the same number ?
-
View Hint View Answer Discuss in Forum
296 + 1 = (232)3 + 13
296 + 1 = (232 + 1) (264 – 232 + 1)Correct Option: A
296 + 1 = (232)3 + 13
296 + 1 = (232 + 1) (264 – 232 + 1)
Clearly, 232 + 1 is a factor of 296 + 1
Hence required answer is 296 + 1 .
- What least number, of 5 digits is divisible by 41?
-
View Hint View Answer Discuss in Forum
As we know that , The least number of 5 digits = 10000
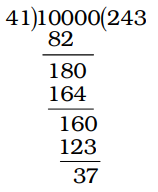
Correct Option: B
As we know that , The least number of 5 digits = 10000
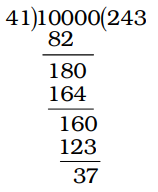
∴ Required number = 10000 + (41 – 37)
Hence Required number = 10004

