Plane Geometry
- In a ∆ ABC, AD, BE and CF are three medians. The perimeter of ∆ ABC is always
-
View Hint View Answer Discuss in Forum
On the basis of given in question , we draw a figure triangle ABC in which AD, BE and CF are three medians ,
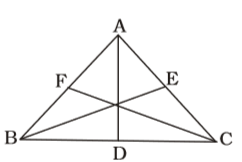
We know that sum of any two sides of a triangle is greater than twice the mediun bisecting the third side.
Here, D, E and F are the midpoint of the sides BC, AC and AB.
∴ AB + AC > 2 AD
AB + BC > 2BE
BC + AC > 2 CF
Adding all three, we getCorrect Option: B
On the basis of given in question , we draw a figure triangle ABC in which AD, BE and CF are three medians ,

We know that sum of any two sides of a triangle is greater than twice the mediun bisecting the third side.
Here, D, E and F are the midpoint of the sides BC, AC and AB.
∴ AB + AC > 2 AD
AB + BC > 2BE
BC + AC > 2 CF
Adding all three, we get
2(AB + BC + AC) > 2(AD + BE + CF)
⇒ AB + BC + AC > AD + BE + CF
-
In a ∆ ABC, AB = BD , ∠B = 70° and ∠C = 50°, thrn ∠ BAD = ? AC DC
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of triangle ABC
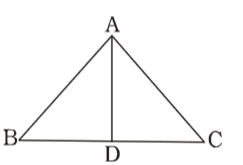
AB = BD AC DC
∴ AD is the bisector of ∠A.∴ ∠BAD = 1 (∠BAC) 2 ∴ ∠BAD = 180 - ∠B - ∠C 2
Correct Option: C
As per the given in question , we draw a figure of triangle ABC

AB = BD AC DC
∴ AD is the bisector of ∠A.∴ ∠BAD = 1 (∠BAC) 2 ∴ ∠BAD = 180 - ∠B - ∠C 2 ∠BAD = 180 - 70 - 50 = 60 = 30° 2 2
- In ∆ABC, D is the mid-point of BC. Length AD is 27 cm. N is a point in AD such that the length of DN is 12 cm. The distance of N from the centroid of ∆ ABC is equal to
-
View Hint View Answer Discuss in Forum
On the basis of given in question , we draw a figure triangle ABC ,
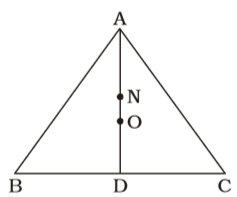
AD = 27 cm
Centroid = O
From figure we know that , AO : OD = 2 : 1∴ OD = 1 AD 3 OD = 1 × 27 = 9 cm 3
Correct Option: A
On the basis of given in question , we draw a figure triangle ABC ,

AD = 27 cm
Centroid = O
From figure we know that , AO : OD = 2 : 1∴ OD = 1 AD 3 OD = 1 × 27 = 9 cm 3
Given , ND = 12 cm
∴ ON = DN – OD = 12 – 9 = 3 cm
- In a ∆ ABC, the medians AD, BE and CF meet at G, then which of the following is true?
-
View Hint View Answer Discuss in Forum
Firstly , We draw a figure of triangle ABC whose the medians AD, BE and CF meet at G ,

In any triangle the sum of the squares of any two sides is equal to twice the square of half of the third side together with twice the square of the median bisecting it.
∴ AB² + AC² = 2(AD² + BD²)
⇒ AB² + AC² = 2(AD² + BC²/4)
⇒ 2(AB² + AC²) = 4 AD² + BC²
Similarly,
2(AB² + BC²) = 4 BE² + AC²
2(AC² + BC²) = 4 CF² + AB²
On adding all three, we get
4(AB² + BC² + AC²) = 4(AD² + BE² + CF²) + BC² + AC² + AB²
⇒ 3(AB² + BC² + AC²) = 4(AD² + BE² + CF²)Correct Option: D
Firstly , We draw a figure of triangle ABC whose the medians AD, BE and CF meet at G ,

In any triangle the sum of the squares of any two sides is equal to twice the square of half of the third side together with twice the square of the median bisecting it.
∴ AB² + AC² = 2(AD² + BD²)
⇒ AB² + AC² = 2(AD² + BC²/4)
⇒ 2(AB² + AC²) = 4 AD² + BC²
Similarly,
2(AB² + BC²) = 4 BE² + AC²
2(AC² + BC²) = 4 CF² + AB²
On adding all three, we get
4(AB² + BC² + AC²) = 4(AD² + BE² + CF²) + BC² + AC² + AB²
⇒ 3(AB² + BC² + AC²) = 4(AD² + BE² + CF²)
Again,
AB + AC > 2AD
AB + BC > 2BE
BC + AC > 2CF
On adding , we get
∴ 2(AB + BC + AC) > 2(AD + BE + CF)
⇒ AB + BC + AC > AD + BE + CF
- AD is the median of a triangle ABC and O is the centroid such that AO = 10 cm. Length of OD (in cm) is
-
View Hint View Answer Discuss in Forum
On the basis of given in question , we draw a figure triangle ABC which AD is the median ,
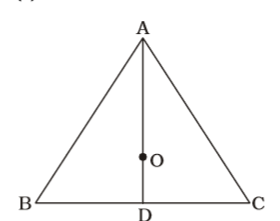
Point ‘O’ is centroid and AD is median.∴ OA = 2 AD 3 ⇒ 10 = 2 AD 3 ⇒ AD = 10 × 3 = 15 cm 2
Correct Option: C
On the basis of given in question , we draw a figure triangle ABC which AD is the median ,

Point ‘O’ is centroid and AD is median.∴ OA = 2 AD 3 ⇒ 10 = 2 AD 3 ⇒ AD = 10 × 3 = 15 cm 2 ∴ OD = 1 AD = 15 = 5 cm 3 3

