Plane Geometry
- In an isosceles ∆ABC, AD is the median to the unequal side meeting BC at D. DP is the angle bisector of ∠ADB and PQ is drawn parallel to BC meeting AC at Q. Then the measure of ∠PDQ is :
-
View Hint View Answer Discuss in Forum
On the basis of given in question , we draw a figure of an isosceles triangle ABC ,

Given AB = AC
Point D is the mid-point of side BC.
∴ ∠ADB = 90° = ∠ADC
PD is internal bisector of ∠ADB.
∴ ∠PDA = 45°Correct Option: B
On the basis of given in question , we draw a figure of an isosceles triangle ABC ,

Given AB = AC
Point D is the mid-point of side BC.
∴ ∠ADB = 90° = ∠ADC
PD is internal bisector of ∠ADB.
∴ ∠PDA = 45°
PQ || BC
∴ ∠ADQ = 45°
∴ PDQ = ∠ADQ + ∠PDA = 45° + 45° = 90°
- In the figure (not drawn to scale) given below, if AD = DC = BC and ∠BCE = 96°, then ∠DBC is :

-
View Hint View Answer Discuss in Forum
From given figure ,

Let ∠ACD = a = ∠DAC
∴ ∠CDB = 2a = ∠CBD
The angles of the base of an isosceles triangle are equal.
∴ ∠ACB = 180° – 96° = 84°
⇒ ∠ACD + ∠DCB = 84°
⇒ a + 180° – 4a = 84°
⇒ 180° – 3a = 84°Correct Option: C
From given figure ,

Let ∠ACD = a = ∠DAC
∴ ∠CDB = 2a = ∠CBD
The angles of the base of an isosceles triangle are equal.
∴ ∠ACB = 180° – 96° = 84°
⇒ ∠ACD + ∠DCB = 84°
⇒ a + 180° – 4a = 84°
⇒ 180° – 3a = 84°
⇒ 3a = 180° – 84° = 96°
⇒ a = 96 ÷ 3 = 32°
⇒ ∠DBC = 2a = 64°
- In an isosceles triangle ∆ ABC, AB = AC and ∠A = 80°. The bisector of∠B and ∠ C meet at D. The ∠BDC is equal to
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of an isosceles triangle ABC

Given that , AB = AC
∴ ∠ABC = ∠ACB
∠A = 80°
∴ ∠B + ∠C = 180° – 80° = 100°
∴ ∠B = 100 ÷ 2 = 50° = ∠CCorrect Option: C
As per the given in question , we draw a figure of an isosceles triangle ABC

Given that , AB = AC
∴ ∠ABC = ∠ACB
∠A = 80°
∴ ∠B + ∠C = 180° – 80° = 100°
∴ ∠B = 100 ÷ 2 = 50° = ∠C
∴ ∠DBC = ∠DCB = 50 ÷ 2 = 25°
∴ ∠BDC = 180° – (∠DBC + ∠DCB) = 180° – 50° = 130°
- The sides of a triangle are in the ratio 3 : 4 : 6. The triangle is :
-
View Hint View Answer Discuss in Forum
Here , The sides of a triangle are in the ratio 3 : 4 : 6
Let the sides of the triangle be 3k, 4k and 6k units.
Clearly, (3k)² + (4k)² < (6k)²Correct Option: C
Here , The sides of a triangle are in the ratio 3 : 4 : 6
Let the sides of the triangle be 3k, 4k and 6k units.
Clearly, (3k)² + (4k)² < (6k)²
∴ The triangle will be obtuse angled.
- O and C are respectively the orthocentre and circumcentre of an acute-angled triangle PQR. The points P and O are joined and produced to meet the side QR at S. If ∠PQS = 60° and ∠QCR = 130°, then ∠RPS=
-
View Hint View Answer Discuss in Forum
On the basis of given in question , we draw a figure with O and C are respectively orthocentre and circumcentre of an acute-angled triangle PQR ,
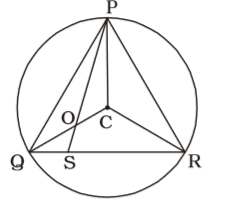
∠ PQS = 60°
∠ QCR = 130°∴ ∠QPR = 1 × 130° = 65° 2
⇒ ∠QRP =180° – 60° – 65° = 55°
⇒ ∠PCQ = 110°
∴ In ∆ QCR,
QC = CR
⇒ ∠CQR = ∠CRQ = 25°
[∵ ∠CQR + ∠CRQ = 50°]
Correct Option: B
On the basis of given in question , we draw a figure with O and C are respectively orthocentre and circumcentre of an acute-angled triangle PQR ,

∠ PQS = 60°
∠ QCR = 130°∴ ∠QPR = 1 × 130° = 65° 2
⇒ ∠QRP =180° – 60° – 65° = 55°
⇒ ∠PCQ = 110°
∴ In ∆ QCR,
QC = CR
⇒ ∠CQR = ∠CRQ = 25°
[∵ ∠CQR + ∠CRQ = 50°]
∴ ∠PQC = ∠QPC = 35°
[∵ ∠PQC + ∠QPC = 70°]
Similarly, ∠ CPR = 30°
∴ ∠RPS = 35°

