Plane Geometry
- If in a triangle ABC, D and E are on the sides AB and AC, such that, DE is parallel to BC and AD / BD = 3 / 5 . If AC = 4 cm, then AE is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of triangle ABC in which D and E are on the sides AB and AC, such that, DE is parallel to BC ,
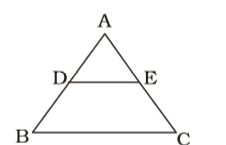
DE || BC ,∴ AD = AE AB AC AD = 3 ⇒ BD = 5 BD 5 AD 3 ⇒ BD + 1 = 5 + 1 AD 3 ⇒ BD + AD = 5 + 3 AD 3 ⇒ AB = 8 AD 3 ⇒ AD = 3 AB 8
Correct Option: A
As per the given in question , we draw a figure of triangle ABC in which D and E are on the sides AB and AC, such that, DE is parallel to BC ,

DE || BC ,∴ AD = AE AB AC AD = 3 ⇒ BD = 5 BD 5 AD 3 ⇒ BD + 1 = 5 + 1 AD 3 ⇒ BD + AD = 5 + 3 AD 3 ⇒ AB = 8 AD 3 ⇒ AD = 3 AB 8 ∴ AD = AE AB AC ⇒ 3 = AE ⇒ AE = 3 × 4 8 4 8
AE = 1.5 cm.
- In a ∆ABC, if 2 ∠ A = 3 ∠ B = 6∠C, value of ∠ B is
-
View Hint View Answer Discuss in Forum
As per the given in question,
∴ 2∠A = 3∠B = 6∠C⇒ 2∠A = 3∠B = 6∠C 6 6 6 ⇒ ∠A = ∠B = ∠C 3 2 1
⇒ ∠A : ∠B : ∠C = 3 : 2 : 1∴ ∠B = 
2 
× 180° 1 + 2 + 3
Correct Option: A
As per the given in question,
∴ 2∠A = 3∠B = 6∠C⇒ 2∠A = 3∠B = 6∠C 6 6 6 ⇒ ∠A = ∠B = ∠C 3 2 1
⇒ ∠A : ∠B : ∠C = 3 : 2 : 1∴ ∠B = 
2 
× 180° 1 + 2 + 3 ∠B = 2 × 180° = 60° 6
- In a ∆ABC, ∠A + ∠B = 70° and ∠B + ∠C = 130°, value of ∠A is
-
View Hint View Answer Discuss in Forum
In ∆ ABC,
As we know that , ∠A + ∠B + ∠C = 180°
Given , ∠A + ∠B = 70° and ∠B + ∠C = 130°Correct Option: B
In ∆ ABC,
As we know that , ∠A + ∠B + ∠C = 180°
Given , ∠A + ∠B = 70° and ∠B + ∠C = 130°
∴ ∠A = (∠A + ∠B + ∠C) – (∠B + ∠C)
∠A = 180– 130°= 50°
- Angle between sss ∠B is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of triangle ABC
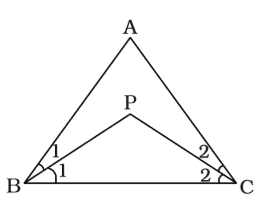
∠BPC = 120°
∴ ∠PBC + ∠PCB = 180°– 120°= 60°Correct Option: D
As per the given in question , we draw a figure of triangle ABC

∠BPC = 120°
∴ ∠PBC + ∠PCB = 180°– 120°= 60°
∴ ∠ABC + ∠ACB = 2 × 60° = 120°
∴ ∠A = 180 – 120 = 60°
- For a triangle ABC, D, E, F are the mid-points of its sides. If ∆ABC = 24 sq. units then ∆DEF is
-
View Hint View Answer Discuss in Forum
On the basis of given in question , we draw a figure triangle ABC ,
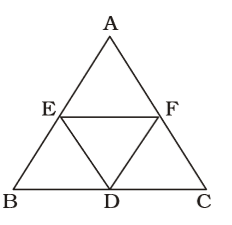
Here , ∆ABC = 24 sq. units
From figure , we have∆DEF = 1 ∆ ABC 4
Correct Option: B
On the basis of given in question , we draw a figure triangle ABC ,

Here , ∆ABC = 24 sq. units
From figure , we have∆DEF = 1 ∆ ABC 4 ∆DEF = 1 × 24 = 6 Sq. unit 4

