Plane Geometry
-
In a ∆ ABC, AB = BD , ∠B = 70° and ∠C = 50°, thrn ∠ BAD = ? AC DC
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of triangle ABC
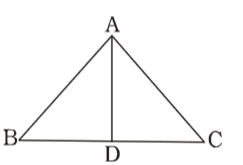
AB = BD AC DC
∴ AD is the bisector of ∠A.∴ ∠BAD = 1 (∠BAC) 2 ∴ ∠BAD = 180 - ∠B - ∠C 2
Correct Option: C
As per the given in question , we draw a figure of triangle ABC

AB = BD AC DC
∴ AD is the bisector of ∠A.∴ ∠BAD = 1 (∠BAC) 2 ∴ ∠BAD = 180 - ∠B - ∠C 2 ∠BAD = 180 - 70 - 50 = 60 = 30° 2 2
- In a ∆ ABC, AD, BE and CF are three medians. The perimeter of ∆ ABC is always
-
View Hint View Answer Discuss in Forum
On the basis of given in question , we draw a figure triangle ABC in which AD, BE and CF are three medians ,
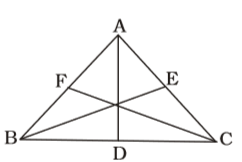
We know that sum of any two sides of a triangle is greater than twice the mediun bisecting the third side.
Here, D, E and F are the midpoint of the sides BC, AC and AB.
∴ AB + AC > 2 AD
AB + BC > 2BE
BC + AC > 2 CF
Adding all three, we getCorrect Option: B
On the basis of given in question , we draw a figure triangle ABC in which AD, BE and CF are three medians ,

We know that sum of any two sides of a triangle is greater than twice the mediun bisecting the third side.
Here, D, E and F are the midpoint of the sides BC, AC and AB.
∴ AB + AC > 2 AD
AB + BC > 2BE
BC + AC > 2 CF
Adding all three, we get
2(AB + BC + AC) > 2(AD + BE + CF)
⇒ AB + BC + AC > AD + BE + CF
- In ∆ABC, ∠A < ∠B. The altitude to the base divides vertex angle C into two parts C1 and C2,with C2,adjacent to BC. Then
-
View Hint View Answer Discuss in Forum
Firstly , We draw a figure of triangle ABC
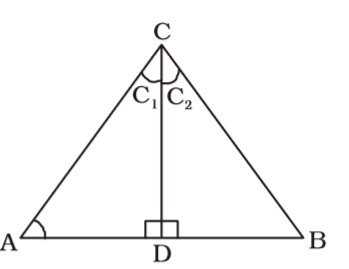
∠BAC < ∠CBA
∠CDA = ∠CDB = 90°; ∠C1 > ∠C2
∠A + ∠C1 = 90°
∠B + ∠C2 = 90°
∴ ∠A + ∠C1 = ∠B + ∠C2Correct Option: C
Firstly , We draw a figure of triangle ABC

∠BAC < ∠CBA
∠CDA = ∠CDB = 90°; ∠C1 > ∠C2
∠A + ∠C1 = 90°
∠B + ∠C2 = 90°
∴ ∠A + ∠C1 = ∠B + ∠C2
∴ ∠B – ∠A = ∠C1 – ∠C2
- If O is the in-centre of ∆ABC; if ∠BOC = 120°, then the measure of ∠BAC is
-
View Hint View Answer Discuss in Forum
On the basis of given in question , we draw a figure triangle ABC ,
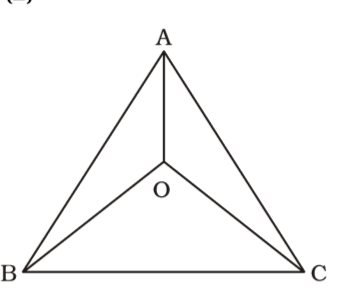
BO, CO and AO are internal bisectors of ∠B, ∠C and ∠A respectively.
Here , ∠BOC = 120°∴ ∠BOC = 90° + ∠A 2 ⇒ 120° = 90° + ∠A 2
Correct Option: B
On the basis of given in question , we draw a figure triangle ABC ,

BO, CO and AO are internal bisectors of ∠B, ∠C and ∠A respectively.
Here , ∠BOC = 120°∴ ∠BOC = 90° + ∠A 2 ⇒ 120° = 90° + ∠A 2 ⇒ ∠A = 120° - 90° = 30° 2
∴ ∠A = 30 × 2 = 60°
- ABC is a triangle and the sides AB, BC and CA are produced to E, F and G respectively. If ∠CBE = ∠ACF = 130° then the value of ∠GAB is
-
View Hint View Answer Discuss in Forum
On the basis of given in question , we draw a figure triangle ABC ,
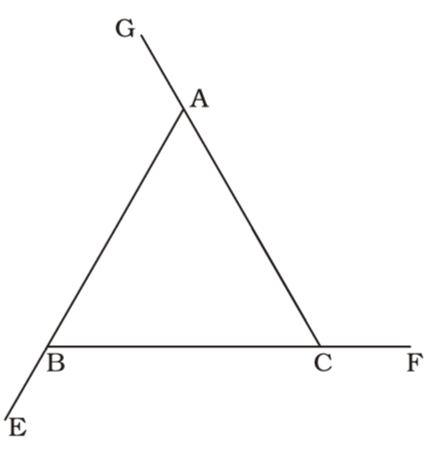
∠CBE = 130°
∴ ∠ABC = 180° – 130° = 50°
∠ACF = 130°
∴ ∠ACB = 180° – 130° = 50°Correct Option: A
On the basis of given in question , we draw a figure triangle ABC ,

∠CBE = 130°
∴ ∠ABC = 180° – 130° = 50°
∠ACF = 130°
∴ ∠ACB = 180° – 130° = 50°
∴ ∠BAC = 180° – 50° – 50° = 80°
∴ ∠GAB = 180° – 80° = 100°

