Plane Geometry
- In a triangle ABC, AB + BC = 12 cm, BC + CA = 14 cm and CA + AB = 18 cm. Find the radius of the circle (in cm) which has the same perimeter as the triangle.
-
View Hint View Answer Discuss in Forum
Given that , AB + BC = 12
BC + CA = 14
CA + AB = 18
On adding , we get
∴ 2(AB + BC + CA) = 12 + 14 + 18 = 44
⇒ AB + BC + CA = 22
∴ 2πr = 22⇒ 2 × 22 × r = 22 7
Correct Option: B
Given that , AB + BC = 12
BC + CA = 14
CA + AB = 18
On adding , we get
∴ 2(AB + BC + CA) = 12 + 14 + 18 = 44
⇒ AB + BC + CA = 22
∴ 2πr = 22⇒ 2 × 22 × r = 22 7 ⇒ r = 7 cm 2
- In ∆ABC, PQ is parallel to BC. If AP : PB = 1 : 2 and AQ = 3 cm; AC is equal to
-
View Hint View Answer Discuss in Forum
Firstly , We draw a figure of triangle ABC ,
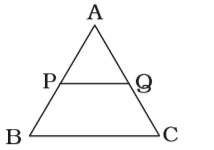
Here , AP : PB = 1 : 2AP = AQ = 1 PB QC 2
Correct Option: B
Firstly , We draw a figure of triangle ABC ,

Here , AP : PB = 1 : 2AP = AQ = 1 PB QC 2 ⇒ QC = 2 ⇒ QC + AQ = 3 AQ 1 AQ 1
⇒ AC = 3AQ = 9 cm
- D is any point on side AC of ABC. If P, Q, X, Y are the midpoints of AB, BC, AD and DC respectively, then the ratio of PX and QY is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of triangle ABC
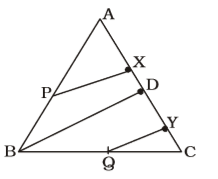
PX || BD and PX = 1 BD 2 QY || BD and QY = 1 BD 2
Correct Option: B
As per the given in question , we draw a figure of triangle ABC

PX || BD and PX = 1 BD 2 QY || BD and QY = 1 BD 2
∴ PX : QY = 1 : 1
- The points D and E are taken on the sides AB and AC of ∆ABC such that AD = 1/3 AB, AE = 1/3 AC. If the length of BC is 15 cm, then the length of DE is :
-
View Hint View Answer Discuss in Forum
On the basis of given in question , we draw a figure triangle ABC ,
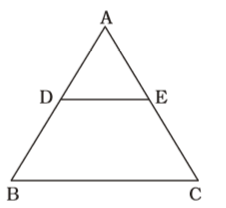
AD = AE = 1 AB AC 3 ∴ DE = 1 BC 3
Correct Option: D
On the basis of given in question , we draw a figure triangle ABC ,

AD = AE = 1 AB AC 3 ∴ DE = 1 BC 3 ⇒ DE = 15 = 5 cm 3
- The external bisector of ∠B and ∠C of ∆ABC (where AB and AC extended to E and F respectively) meet at point P. If ∠BAC = 100°, then the measure of ∠BPC is
-
View Hint View Answer Discuss in Forum
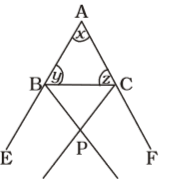
In &&8710;ABC
∠A = x, ∠B = y; ∠C = z
In ∆PBC,
∠PBC + ∠PCB + ∠BPC = 180°Correct Option: C

In &&8710;ABC
∠A = x, ∠B = y; ∠C = z
In ∆PBC,
∠PBC + ∠PCB + ∠BPC = 180°

