Plane Geometry
- In a triangle ABC, the side BC is extended up to D. Such that CD = AC, if ∠BAD = 109° and ∠ACB = 72° then the value of ∠ABC is
-
View Hint View Answer Discuss in Forum
On the basis of given in question , we draw a figure triangle ABC ,
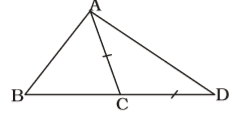
∠ACD = 180° – ∠ACB (Linear Pair)
∠ACD = 180° – 72° = 108°∠CAD = ∠ADC = 72 = 36 cm 2
Correct Option: A
On the basis of given in question , we draw a figure triangle ABC ,

∠ACD = 180° – ∠ACB (Linear Pair)
∠ACD = 180° – 72° = 108°∠CAD = ∠ADC = 72 = 36 cm 2
∴ ∠ABC = 180° – 109° – 36° = 35°
- ABC is a triangle. The bisectors of the internal angle ∠B and external angle ∠C intersect at D. If ∠BDC= 50°, then ∠A is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of triangle ABC in which bisectors of the internal angle ∠B and external angle ∠C intersect at point D ,
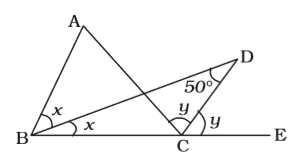
[Exterior angle is sum of opp. interior angles]
∠ACE = ∠BAC + ∠ABC
⇒ 2y = ∠A + 2x
Similarly ,
∠DCE = ∠DBC + ∠BDCCorrect Option: A
As per the given in question , we draw a figure of triangle ABC in which bisectors of the internal angle ∠B and external angle ∠C intersect at point D ,

[Exterior angle is sum of opp. interior angles]
∠ACE = ∠BAC + ∠ABC
⇒ 2y = ∠A + 2x
Similarly ,
∠DCE = ∠DBC + ∠BDC
⇒ y = 50° + x
⇒ ∠A = 2y – 2x = 100 + 2x – 2x = 100°
- If the length of the sides of a triangle are in the ratio 4 : 5 : 6 and the inradius of the triangle is 3 cm, then the altitude of the triangle corresponding to the largest side as base is :
-
View Hint View Answer Discuss in Forum
On the basis of given in question , we draw a figure a triangle ABC ,
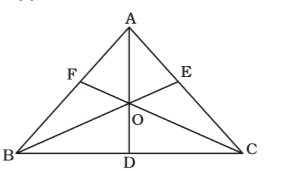
The ratio of the sides of a triangle = 4 : 5 : 6
Let AB = 4y , BC = 5y , CA = 6y
∆OBA + ∆BOC + ∆AOC = ∆ABC⇒ 1 × 4y ×3 + 1 × 5y × 3 + 1 × 6y ×3 = 1 × 6y × h 2 2 2 2 ⇒ 6y + 15y + 9y = 3yh 2
Correct Option: A
On the basis of given in question , we draw a figure a triangle ABC ,

The ratio of the sides of a triangle = 4 : 5 : 6
Let AB = 4y , BC = 5y , CA = 6y
∆OBA + ∆BOC + ∆AOC = ∆ABC⇒ 1 × 4y ×3 + 1 × 5y × 3 + 1 × 6y ×3 = 1 × 6y × h 2 2 2 2 ⇒ 6y + 15y + 9y = 3yh 2
⇒ 12 + 15 + 18 = 6h
⇒ 45 = 6h⇒ h = 15 = 7.5 cm 2
- Taking any three of the line segments out of segments of length 2 cm, 3 cm, 5 cm and 6 cm, the number of triangles that can be formed is :
-
View Hint View Answer Discuss in Forum
According to question ,
The sum of two sides of a triangle should be greater than the third side.Correct Option: B
According to question ,
The sum of two sides of a triangle should be greater than the third side.
(3, 5, 6) and (2, 5, 6)
- If the circumcentre of a triangle lies outside it, then the triangleis
-
View Hint View Answer Discuss in Forum
As we know that the right bisectors of the sides of a triangle meet at a point. The point of intersection is called circum-centre.
Correct Option: D
As we know that the right bisectors of the sides of a triangle meet at a point. The point of intersection is called circum-centre. For an obtuse angled triangle, circum-centre lies outside the triangle.

