We draw a figure triangle ABC whose the medians BD, CE and AFmeet at point G ,

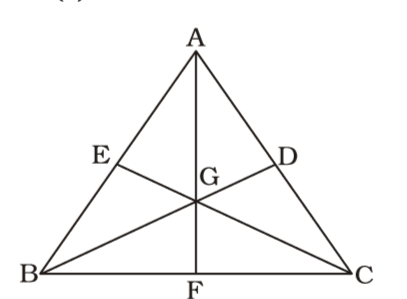
Point G is the centroid of ∆ ABC.
Point G divides AF (each median) in the ratio 2 : 1.
Proof :-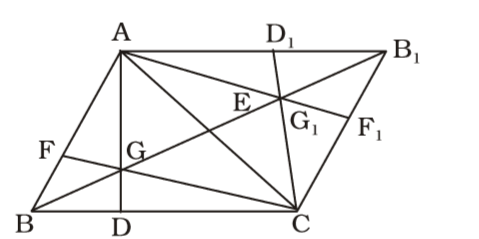

Reflect ∆ ABC on side AC.
ABCB₁ is a parallelogram.
BEB₁ is a straight line. and
∵ CD = AD, and CD || AD₁
DCD₁A is a parallelogram.
DG || CG₁

Correct Option: B

We draw a figure triangle ABC whose the medians BD, CE and AFmeet at point G ,

Point G is the centroid of ∆ ABC.
Point G divides AF (each median) in the ratio 2 : 1.
Proof :-

Reflect ∆ ABC on side AC.
ABCB₁ is a parallelogram.
BEB₁ is a straight line. and
∵ CD = AD, and CD || AD₁
DCD₁A is a parallelogram.
DG || CG₁
∵ BD = DC and DG || CG, and BG = GG₁
∴ BG : GG₁ = 1 : 1
∵ GE = EG₁, BG = GE = 2 : 1

We draw a figure triangle ABC whose the side AD is the median and O is the centroid ,

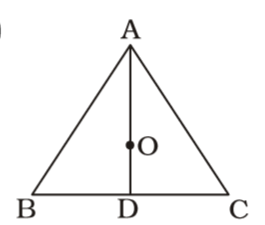
Here , AO = 10 cm
Point O, is the centroid of ∆ ABC.
AO : OD = 2 : 1

Correct Option: A

We draw a figure triangle ABC whose the side AD is the median and O is the centroid ,

Here , AO = 10 cm
Point O, is the centroid of ∆ ABC.
AO : OD = 2 : 1

We know that the sum of two sides of a triangle is greater than the third side.
Clearly,
3 + 4 > 5
4 + 5 > 3
5 + 3 > 4

Correct Option: B

We know that the sum of two sides of a triangle is greater than the third side.
Clearly,
3 + 4 > 5
4 + 5 > 3
5 + 3 > 4
Therefore , Possible lengths of the three sides of a triangle are 3 cm, 4 cm and 5 cm .

According to question , we draw a figure

Given , AB = a – b; BC = √2ab ;
AC = √a² + b²
∴ AB² + BC² = (a – b)² + (√2ab)²

Correct Option: C

According to question , we draw a figure

Given , AB = a – b; BC = √2ab ;
AC = √a² + b²
∴ AB² + BC² = (a – b)² + (√2ab)²
AB² + BC² = a² + b² – 2ab + 2ab = a² + b² = AC²
∴ ∠ABC = 90°

Given that , EO = 7cm,
Point ‘O’ is the centroid of triangle ABC.

Correct Option: C

Given that , EO = 7cm,
Point ‘O’ is the centroid of triangle ABC.