Plane Geometry
- A man goes 24 m due west and then 10 m due north. Then the distance of him from the starting point is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of triangle ABC

∠ABC = 90°
Given , AB = 24 metre , BC = 10 metre
∴ AC = √AB² + BC²
AC = √24² + 10²Correct Option: B
As per the given in question , we draw a figure of triangle ABC

∠ABC = 90°
Given , AB = 24 metre , BC = 10 metre
∴ AC = √AB² + BC²
AC = √24² + 10²
AC = √576 + 100
AC = √676 = 26 metre
- In ∆ABC, ∠C is an obtuse angle. The bisectors of the exterior angles at A and B meet BC and AC produced at D and E respectively. If AB = AD = BE, then ∠ACB =
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of triangle ABC
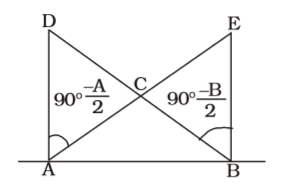
∠DAC = 1 (180° - A) = 90° – ∠ A 2 2
In ∆ADB,
∠DAB + ∠ADB + ∠DBA = 180°⇒90° – ∠ A + ∠A + 2 ∠B = 180° 2
[∵ AD = AB ⇒ ∠ADB = ∠DBA = ∠B]⇒90° + ∠ A + 2 ∠B = 180° 2
⇒ ∠A + 4∠B = 180° ....(i)
In ∆ABE,
AB = BE
∴ ∠BAE = ∠AEB
∴ ∠ABE + ∠BAE + ∠BEA = 180°⇒90° - ∠B + ∠B + 2∠A = 180° 2 ⇒90° + ∠B + 2 ∠A = 180° 2
⇒ ∠B + 4∠A = 180° ....(ii)
From equations (i) and (ii),
∠A + 4∠B = 4∠A + ∠B
⇒ 3∠A = 3∠B
⇒ ∠A = ∠B
∴ ∠A + 4∠B = 180°
⇒ 5∠B = 180°
Correct Option: B
As per the given in question , we draw a figure of triangle ABC

∠DAC = 1 (180° - A) = 90° – ∠ A 2 2
In ∆ADB,
∠DAB + ∠ADB + ∠DBA = 180°⇒90° – ∠ A + ∠A + 2 ∠B = 180° 2
[∵ AD = AB ⇒ ∠ADB = ∠DBA = ∠B]⇒90° + ∠ A + 2 ∠B = 180° 2
⇒ ∠A + 4∠B = 180° ....(i)
In ∆ABE,
AB = BE
∴ ∠BAE = ∠AEB
∴ ∠ABE + ∠BAE + ∠BEA = 180°⇒90° - ∠B + ∠B + 2∠A = 180° 2 ⇒90° + ∠B + 2 ∠A = 180° 2
⇒ ∠B + 4∠A = 180° ....(ii)
From equations (i) and (ii),
∠A + 4∠B = 4∠A + ∠B
⇒ 3∠A = 3∠B
⇒ ∠A = ∠B
∴ ∠A + 4∠B = 180°
⇒ 5∠B = 180°⇒ ∠B = 180 = 36° = ∠A 5
∴ ∠ACB = 180° – 36° – 36°
∠ACB = 180° – 72° = 108°
- If two angles of a triangle are 21° and 38°, then the triangle is
-
View Hint View Answer Discuss in Forum
Given , two angles of a triangle are 21° and 38°
We know that , Sum of three angles of triangle = 180°
Third angle of triangle = 180° – (21° + 38°)Correct Option: C
Given , two angles of a triangle are 21° and 38°
We know that , Sum of three angles of triangle = 180°
Third angle of triangle = 180° – (21° + 38°)
Third angle of triangle = 180° – 59° = 121° > 90°
i.e., It is an obtuse angle .
- I is the incentre of a triangle ABC. If ∠ABC = 65° and ∠ACB = 55°, then the value of ∠BIC is
-
View Hint View Answer Discuss in Forum
Firstly , We draw a figure of triangle ABC whose I is incentre ,
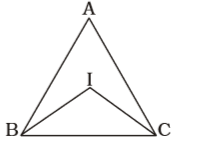
∠IBC = 1 ∠ABC = 65 = 32.5° 2 2 ∠ICB = 1 ∠ACB = 55 = 27.5° 2 2
Correct Option: B
Firstly , We draw a figure of triangle ABC whose I is incentre ,

∠IBC = 1 ∠ABC = 65 = 32.5° 2 2 ∠ICB = 1 ∠ACB = 55 = 27.5° 2 2
We know that , ∠BIC + ∠ICB + ∠IBC = 180°
∴ ∠BIC = 180° - 32.5° - 27.5° = 120°
- I is the incentre of ∆ABC, ∠ABC = 60° and ∠ACB = 50°. Then ∠BIC is :
-
View Hint View Answer Discuss in Forum
On the basis of given in question , we draw a figure triangle ABC ,
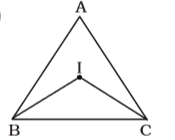
∠ABC = 60°, ACB = 50°∠IBC = 1 ∠ABC = 30° 2 ∠ICB = 1 ∠ACB = 25° 2
Correct Option: B
On the basis of given in question , we draw a figure triangle ABC ,

∠ABC = 60°, ACB = 50°∠IBC = 1 ∠ABC = 30° 2 ∠ICB = 1 ∠ACB = 25° 2
We know that , ∠BIC + ∠ICB + ∠IBC = 180°
∴ ∠BIC = 180° – 30° – 25° = 125°

