Plane Geometry
- Each interior angle of a regular polygon is 144°. The number of sides of the polygon is
-
View Hint View Answer Discuss in Forum
If the number of sides of the polygon be n, then
As per the given in question ,
Each interior angle of a regular polygon = 144°
2n - 4 
× 90° = 144° n ⇒ (2n - 4)5 = 8 n
Correct Option: C
If the number of sides of the polygon be n, then
As per the given in question ,
Each interior angle of a regular polygon = 144°
2n - 4 
× 90° = 144° n ⇒ (2n - 4)5 = 8 n
⇒ 10n – 20 = 8n
⇒ 2n = 20
⇒ n = 10
- In a regular polygon, the exterior and interior angles are in the ratio 1 : 4. The number of sides of the polygon is
-
View Hint View Answer Discuss in Forum
Given , The ratio of exterior and interior angles = 1 : 4
Let the exterior angle be y, then interior angle will be 4y.
We know that , Interior angle + Exterior angle = 180°
∴ y + 4y = 180°⇒ y = 180 = 36° 5
∴ Interior angle = 4y = 4 × 36° = 144°Interior angle of a polygon = 2n - 4 × 90° n 144° = 2n - 4 × 90° n
Correct Option: A
Given , The ratio of exterior and interior angles = 1 : 4
Let the exterior angle be y, then interior angle will be 4y.
We know that , Interior angle + Exterior angle = 180°
∴ y + 4y = 180°⇒ y = 180 = 36° 5
∴ Interior angle = 4y = 4 × 36° = 144°Interior angle of a polygon = 2n - 4 × 90° n 144° = 2n - 4 × 90° n
⇒ 144°n = 180°n – 360°
⇒ 180°n – 144n = 360°
⇒ 36°n = 360°∴ n = 360° = 10 36°
- In ∆ ABC and ∆ DEF, AB = DE and BC = EF. Then one can infer that ∆ ABC ≅ ∆ DEF, when
-
View Hint View Answer Discuss in Forum
According to question , we draw figures of two similar triangles ABC and DEF

Two triangles are congruent if two sides and the included angle of one are equal to the corresponding sides and the included angle of the other triangle.Correct Option: D
According to question , we draw figures of two similar triangles ABC and DEF

Two triangles are congruent if two sides and the included angle of one are equal to the corresponding sides and the included angle of the other triangle.
This is called SAS criterion .
- In a right-angled triangle ABC, ∠ABC = 90°, AB = 5 cm and BC = 12 cm. The radius of the circumcircle of the triangle ABC is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure right-angled triangle ABC ,
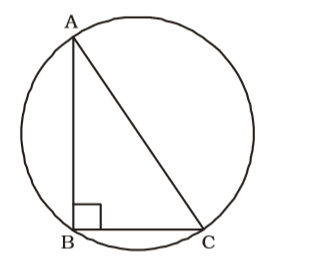
Given that , ∠ABC = 90°, AB = 5 cm and BC = 12 cm.
AC = Diameter of circum circle = √AB² + BC²
Correct Option: C
As per the given in question , we draw a figure right-angled triangle ABC ,

Given that , ∠ABC = 90°, AB = 5 cm and BC = 12 cm.
AC = Diameter of circum circle = √AB² + BC²
AC = √5² + 12² = 13 cm
∴ Circum-radius = 13 ÷ 2 = 6.5 cm
- For a triangle, base is 6√3 cm and two base angles are 30° and 60°. Then height of the triangle is
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of triangle ABC ,
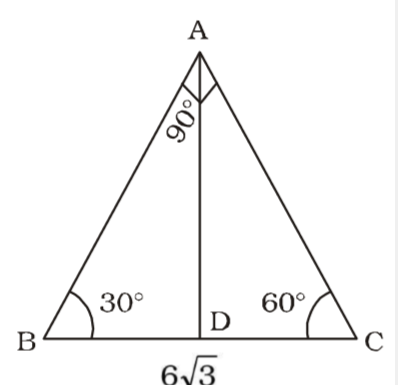
sin30° = AC BC ⇒ 1 = AC ⇒ AC = 3√3 2 6√3 Also, sin60° = AD AC ⇒ √3 = AD 2 3√3
Correct Option: B
On the basis of question we draw a figure of triangle ABC ,

sin30° = AC BC ⇒ 1 = AC ⇒ AC = 3√3 2 6√3 Also, sin60° = AD AC ⇒ √3 = AD 2 3√3 ⇒ AD = 3√3 × √3 = 4.5 cm. 2

