Plane Geometry
- In a ∆ABC, if 2 ∠ A = 3 ∠ B = 6∠C, value of ∠ B is
-
View Hint View Answer Discuss in Forum
As per the given in question,
∴ 2∠A = 3∠B = 6∠C⇒ 2∠A = 3∠B = 6∠C 6 6 6 ⇒ ∠A = ∠B = ∠C 3 2 1
⇒ ∠A : ∠B : ∠C = 3 : 2 : 1∴ ∠B = 
2 
× 180° 1 + 2 + 3
Correct Option: A
As per the given in question,
∴ 2∠A = 3∠B = 6∠C⇒ 2∠A = 3∠B = 6∠C 6 6 6 ⇒ ∠A = ∠B = ∠C 3 2 1
⇒ ∠A : ∠B : ∠C = 3 : 2 : 1∴ ∠B = 
2 
× 180° 1 + 2 + 3 ∠B = 2 × 180° = 60° 6
- In a ∆ABC, ∠A + ∠B = 70° and ∠B + ∠C = 130°, value of ∠A is
-
View Hint View Answer Discuss in Forum
In ∆ ABC,
As we know that , ∠A + ∠B + ∠C = 180°
Given , ∠A + ∠B = 70° and ∠B + ∠C = 130°Correct Option: B
In ∆ ABC,
As we know that , ∠A + ∠B + ∠C = 180°
Given , ∠A + ∠B = 70° and ∠B + ∠C = 130°
∴ ∠A = (∠A + ∠B + ∠C) – (∠B + ∠C)
∠A = 180– 130°= 50°
- Angle between sss ∠B is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of triangle ABC
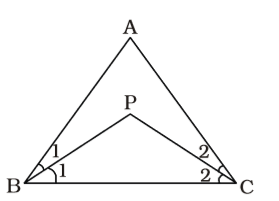
∠BPC = 120°
∴ ∠PBC + ∠PCB = 180°– 120°= 60°Correct Option: D
As per the given in question , we draw a figure of triangle ABC

∠BPC = 120°
∴ ∠PBC + ∠PCB = 180°– 120°= 60°
∴ ∠ABC + ∠ACB = 2 × 60° = 120°
∴ ∠A = 180 – 120 = 60°
- For a triangle ABC, D, E, F are the mid-points of its sides. If ∆ABC = 24 sq. units then ∆DEF is
-
View Hint View Answer Discuss in Forum
On the basis of given in question , we draw a figure triangle ABC ,
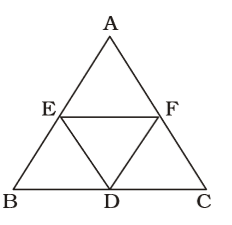
Here , ∆ABC = 24 sq. units
From figure , we have∆DEF = 1 ∆ ABC 4
Correct Option: B
On the basis of given in question , we draw a figure triangle ABC ,

Here , ∆ABC = 24 sq. units
From figure , we have∆DEF = 1 ∆ ABC 4 ∆DEF = 1 × 24 = 6 Sq. unit 4
- If I be the incentre of ∆ ABC and ∠B = 70° and ∠C = 50°, then the magnitude of ∠BIC is
-
View Hint View Answer Discuss in Forum
Firstly , We draw a figure of triangle ABC whose I is incentre ,
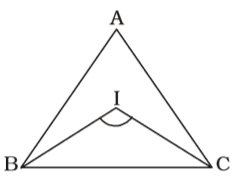
Here , ∠B = 70° and ∠C = 50°∠IBC = 70° = 35° ; 2 ∠ICB = 50° = 25° ; 2
Correct Option: C
Firstly , We draw a figure of triangle ABC whose I is incentre ,

Here , ∠B = 70° and ∠C = 50°∠IBC = 70° = 35° ; 2 ∠ICB = 50° = 25° ; 2
We know that , ∠BIC + ∠ICB + ∠IBC = 180°
∴ ∠BIC = 180° – 35° – 25°
∠BIC = 180° – 60° = 120°

