Plane Geometry

Plane Geometry

Easy Questions
Moderate Questions
Difficult Questions
Plane Geometry Tutorial

Aptitude

Simplification
Number System
Fractions
Elementary Algebra
LCM and HCF
Approximation
Unitary Method
Linear Equation
Quadratic Equation
Discount
Average
Surds and Indices
Percentage
Square root and cube root
Order of Magnitude
Work and Wages
Odd Man Out and Series
Algebra
Profit and Loss
Stocks and Shares
True Discount
Ratio, Proportion
Partnership
Alligation or Mixture
Time and Work
Pipes and Cistern
Speed, Time and Distance
Problem on Trains
Height and Distance
Banker's Discount
Boats and Streams
Races and games
Problems on Ages
Clocks and Calendars
Simple interest
Compound Interest
Sets and Functions
Area and Perimeter
Volume and Surface Area of Solid Figures
Sequences and Series
Plane Geometry
Logarithm
Probability
Permutation and Combination
Statistics
Mensuration
Trigonometry
Aptitude miscellaneous
  1. O is the in-centre of the ∆ABC, if ∠BOC = 116°, then ∠BAC is








  1. View Hint View Answer Discuss in Forum

    On the basis of given in question , we draw a figure triangle ABC in which O is the in-centre ,

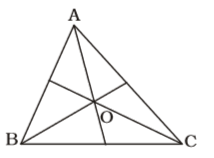
    The point of intersection of internal bisectors of a triangle is called in-centre.

    ∠BOC = 90° +
    ∠A
    2

    ⇒ 116° = 90° +
    ∠A
    2

    Correct Option: D

    On the basis of given in question , we draw a figure triangle ABC in which O is the in-centre ,

    The point of intersection of internal bisectors of a triangle is called in-centre.

    ∠BOC = 90° +
    ∠A
    2

    ⇒ 116° = 90° +
    ∠A
    2

    ⇒
    ∠A
    		 = 116° - 90° = 26°
    2

    ∴ ∠A = 26 × 2 = 52°

  1. The equidistant point from the vertices of a triangle is called its :








  1. View Hint View Answer Discuss in Forum

    As we know that the right bisectors of sides meet at a point called circumcentre.

    Correct Option: C

    As we know that the equidistant point from the vertices of a triangle is called circumcentre.
    Or The right bisectors of sides meet at a point called circumcentre.

  1. In a triangle ABC, incentre is O and ∠BOC = 110°, then the measure of ∠BAC is :








  1. View Hint View Answer Discuss in Forum

    As per the given in question , we draw a figure of triangle ABC

    ∠BOC = 90° +
    ∠A
    2

    Correct Option: B

    As per the given in question , we draw a figure of triangle ABC

    ∠BOC = 90° +
    ∠A
    2

    ⇒ 110 = 90° +
    ∠A
    2

    ⇒ ∠A = 2 × 20 = 40°

  1. Let O be the in-centre of a triangle ABC and D be a point on the side BC of ∆ABC, such that OD ⊥ BC. If ∠BOD = 15°, then ∠ABC =








  1. View Hint View Answer Discuss in Forum

    Firstly , We draw a figure of triangle ABC whose O be the in-centre ,

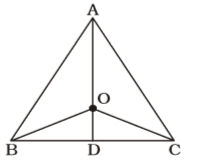
    BO is the internal bisector of ∠B
    ∠ODB = 90°; ∠BOD = 15°

    Correct Option: C

    Firstly , We draw a figure of triangle ABC whose O be the in-centre ,

    BO is the internal bisector of ∠B
    ∠ODB = 90°; ∠BOD = 15°
    ∴ ∠OBD = 180° – 90° – 15° = 75°
    ⇒ ∠ABC = 2 × 75° = 150°

  1. O is the incentre of ∆ABC and ∠A = 30°, then ∠BOC is








  1. View Hint View Answer Discuss in Forum

    On the basis of given in question , we draw a figure triangle ABC ,

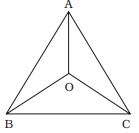
    Given that , ∠BAC = 30°

    Correct Option: B

    On the basis of given in question , we draw a figure triangle ABC ,

    Given that , ∠BAC = 30°

    Now, ∠BOC = 90° +
    1
    		 ∠BAC
    2

    ∠BOC = 90° + 15° = 105°