Plane Geometry
- N is the foot of the perpendicular from a point P of a circle with radius 7 cm, on a diameter AB of the circle. If the length of the chord PB is 12 cm, the distance of the point N from the point B is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure a circle,

AB = 14 cm, PB = 12 cm
∠APB = 90° (angle in the semi circle)
∴ AP = √14² - 12²
AP = √(14 + 12)(14 - 12)
AP = √26 × 2 = √52
Let AN = y ⇒ NB = 14 – y
In ∆ APN, PN² = AP² – AN² = 52 – y² ...(i)
In ∆ PNB, PN² = PB² – NB² = 12² – (14 – y)² ...(ii)
From (i) and (ii)
52 – y² = 144 – (14 – y)²
52 – y² = 144 – (196 + y² – 28 y)
⇒ 52 – y² = 144 –196 – y² + 28 y
52 = – 52 + 28 y⇒ 28 y = 104 ⇒ y = 104 = 26 28 7
NB = 14 – y
Correct Option: D
As per the given in question , we draw a figure a circle,

AB = 14 cm, PB = 12 cm
∠APB = 90° (angle in the semi circle)
∴ AP = √14² - 12²
AP = √(14 + 12)(14 - 12)
AP = √26 × 2 = √52
Let AN = y ⇒ NB = 14 – y
In ∆ APN, PN² = AP² – AN² = 52 – y² ...(i)
In ∆ PNB, PN² = PB² – NB² = 12² – (14 – y)² ...(ii)
From (i) and (ii)
52 – y² = 144 – (14 – y)²
52 – y² = 144 – (196 + y² – 28 y)
⇒ 52 – y² = 144 –196 – y² + 28 y
52 = – 52 + 28 y⇒ 28 y = 104 ⇒ y = 104 = 26 28 7
NB = 14 – yNB = 14 – 26 = 72 = 10 2 cm. 7 7 7
- The length of the common chord of two intersecting circles is 24 cm. If the diameter of the circles are 30 cm and 26 cm, then the distance between the centre (in cm) is
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of two circles with centres O and O' ,
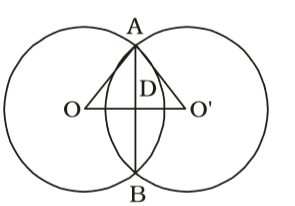
Here , d1 = 30 cm and d1 = 30 cm
From ∆AOD and ∆AO'D ,
OD = √15² - 12²
OD = √225 - 144
OD = √81 = 9 cm
O'D = √13² + 12²
O'D = √169 - 144Correct Option: B
On the basis of question we draw a figure of two circles with centres O and O' ,

Here , d1 = 30 cm and d1 = 30 cm
From ∆AOD and ∆AO'D ,
OD = √15² - 12²
OD = √225 - 144
OD = √81 = 9 cm
O'D = √13² + 12²
O'D = √169 - 144
O'D = √25
O'D = 5 cm
∴ OƠ = OD + O'D = 9 + 5 = 14 cm
- One chord of a circle is known to be 10.1 cm. The radius of this circle must be:
-
View Hint View Answer Discuss in Forum
The largest chord of a circle is its diameter.
Correct Option: B
As we can say that the largest chord of a circle is its diameter.
- The side AB of a parallelogram ABCD is produced to E in such way that BE = AB. DE intersects BC at Q. The point Q divides BC in the ratio
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of parallelogram ABCD in which side AB is produced to E in such way that BE = AB. DE intersects BC at Q ,
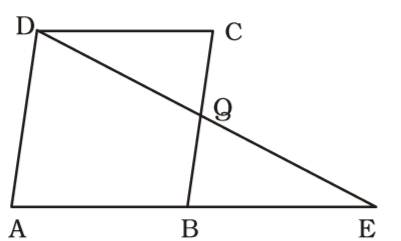
AD || BC ⇒ AD || BQ
Point B is the mid-point of AE.
∴ Q is the mid-point of DE.
In &8710;s DQC and BQE,
∠DQC = ∠BQE
∠DCQ = ∠QBE
∠CDQ = ∠QEB
∴ Both triangles ∆ DQC and ∆ BQE are similar.Correct Option: B
On the basis of question we draw a figure of parallelogram ABCD in which side AB is produced to E in such way that BE = AB. DE intersects BC at Q ,

AD || BC ⇒ AD || BQ
Point B is the mid-point of AE.
∴ Q is the mid-point of DE.
In &8710;s DQC and BQE,
∠DQC = ∠BQE
∠DCQ = ∠QBE
∠CDQ = ∠QEB
∴ Both triangles ∆ DQC and ∆ BQE are similar.∴ DQ = CQ = 1 : 1 QE BQ
- If the ratio of an external angle and an internal angle of a regular polygon is 1 : 17, then the number of sides of the regular polygon is
-
View Hint View Answer Discuss in Forum
Given that , the ratio of an external angle and an internal angle = 1 : 17
Let Number of sides of regular polygon = n
According to question,Exterior angle = 1 Interior angle 17 ⇒ 360 n = 1 (2n - 4) × 90° 17 n ⇒ 4 = 1 2n - 4 17
⇒ 2n – 4 = 4 × 17
⇒ 2n – 4 = 68
Correct Option: C
Given that , the ratio of an external angle and an internal angle = 1 : 17
Let Number of sides of regular polygon = n
According to question,Exterior angle = 1 Interior angle 17 ⇒ 360 n = 1 (2n - 4) × 90° 17 n ⇒ 4 = 1 2n - 4 17
⇒ 2n – 4 = 4 × 17
⇒ 2n – 4 = 68
⇒ 2n = 68 + 4 = 72⇒ n = 72 = 36 2

