Plane Geometry
- If the length of a chord of a circle is equal to that of the radius of the circle, then the angle subtended, in radians, at the centre of the circle by the chord is
-
View Hint View Answer Discuss in Forum
We draw a figure with the details in question ,

According to the question,
OA = AB = OB
∴ ∆ OAB is an equilateral triangle.
∴ ∠AOB = 60°
∵ 180° = π radianCorrect Option: C
We draw a figure with the details in question ,

According to the question,
OA = AB = OB
∴ ∆ OAB is an equilateral triangle.
∴ ∠AOB = 60°
∵ 180° = π radian∴ 60° = π × 60 = π radian 180 2
- Two circles of radii 10 cm and 8 cm intersect and the length of the common chord is 12 cm. Then the distance between their centres is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of two circles with centres O and O' ,
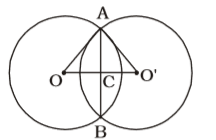
Given that , AB = 12 cm
AC = BC = 6 cm
OA = 10 cm
From ∆ AOC,
∴ OC = √OA² - AC²
OC = √10² - 6² = √100 - 36
OC = √64 = 8 cm
Again, in ∆ ACO',
AO' = 8 cmCorrect Option: C
As per the given in question , we draw a figure of two circles with centres O and O' ,

Given that , AB = 12 cm
AC = BC = 6 cm
OA = 10 cm
From ∆ AOC,
∴ OC = √OA² - AC²
OC = √10² - 6² = √100 - 36
OC = √64 = 8 cm
Again, in ∆ ACO',
AO' = 8 cm
∴ O'C = √8² - 6²
O'C = √64 - 36 = √28 = 5.3 cm
∴ OO' = OC + CO'
OO' = 8 + 5.3 = 13.3 cm
- Two circles C1 and C2 touch each other internally at P. Two lines PCA and PDB meet the circles C1 in C, D and C2 in A, B respectively. If ∠BDC = 120°, then the value of ∠ABP is equal to
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of two circles C1 and C2 touch each other internally at P ,
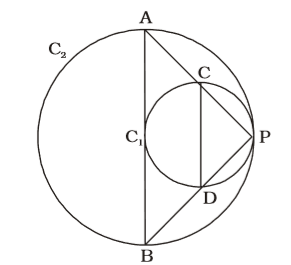
Given , ∠BDC = 120°Correct Option: A
On the basis of question we draw a figure of two circles C1 and C2 touch each other internally at P ,

Given , ∠BDC = 120°
∴ ∠CDP = 180° – 120° = 60°
CD || AB
∴ ∠ABP = 60° = ∠CDP
- Two circles touch externally at P. QR is a common tangent of the circles touching the circles at Q and R. Then measure of ∠QPR is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of two circles touch externally at P and QR is a common tangent of the circles touching the circles at Q and R ,
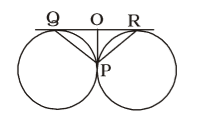
OQ = OP = OR
(Tangents drawn from the same external point)
∴ ∠ QPO = ∠ PQO = ∠ OPRCorrect Option: C
As per the given in question , we draw a figure of two circles touch externally at P and QR is a common tangent of the circles touching the circles at Q and R ,

OQ = OP = OR
(Tangents drawn from the same external point)
∴ ∠ QPO = ∠ PQO = ∠ OPR
= ∠ PRO = 45° because ∠ POQ
= ∠ POR = 90°
∴ ∠ QPR = 45° + 45° = 90°
- If the chord of a circle is equal to the radius of the circle, then the angle subtended by the chord at a point on the minor arc is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure a circle,

OA = OB = ABCorrect Option: B
As per the given in question , we draw a figure a circle,

OA = OB = AB
∴ ∆ OAB is an equilateral triangle.
Hence, ∠AOB = 60°

