Plane Geometry
- In an isosceles ∆ABC, AD is the median to the unequal side meeting BC at D. DP is the angle bisector of ∠ADB and PQ is drawn parallel to BC meeting AC at Q. Then the measure of ∠PDQ is :
-
View Hint View Answer Discuss in Forum
On the basis of given in question , we draw a figure of an isosceles triangle ABC ,

Given AB = AC
Point D is the mid-point of side BC.
∴ ∠ADB = 90° = ∠ADC
PD is internal bisector of ∠ADB.
∴ ∠PDA = 45°Correct Option: B
On the basis of given in question , we draw a figure of an isosceles triangle ABC ,

Given AB = AC
Point D is the mid-point of side BC.
∴ ∠ADB = 90° = ∠ADC
PD is internal bisector of ∠ADB.
∴ ∠PDA = 45°
PQ || BC
∴ ∠ADQ = 45°
∴ PDQ = ∠ADQ + ∠PDA = 45° + 45° = 90°
- ∆ABC is an isosceles triangle with AB = AC = 15 cm and altitude from A to BC is 12 cm. The length of side BC is :
-
View Hint View Answer Discuss in Forum
We draw a figure of an isosceles triangle ABC ,
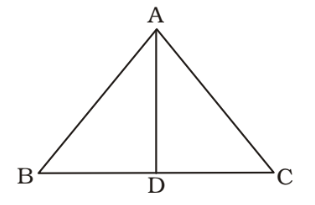
Here , AB = AC = 15 cm.
AD ⊥ BC ; AD = 12 cm.
∴ BD = DC
In, ∆ABD
BD = √AB² - AD²
BD = √15² - 12²
BD = √(15 + 12)(15 – 12)Correct Option: C
We draw a figure of an isosceles triangle ABC ,

Here , AB = AC = 15 cm.
AD ⊥ BC ; AD = 12 cm.
∴ BD = DC
In, ∆ABD
BD = √AB² - AD²
BD = √15² - 12²
BD = √(15 + 12)(15 – 12)
BD = √27 × 3 = 9 cm.
∴ BC = 2 × BD = 2 × 9 = 18 cm.
- In an isosceles triangle ABC, AB = AC, XY ||BC. IfÐA = 30°, then ∠BXY = ?
-
View Hint View Answer Discuss in Forum
On the basis of given in question , we draw a figure of an isosceles triangle ABC ,

∆ ABC is an isosceles triangle.
∴ ∠ABC = ∠ACB { ∴ AB = AC }∠ABC = 180° - 30° = 75° 2
Correct Option: D
On the basis of given in question , we draw a figure of an isosceles triangle ABC ,

∆ ABC is an isosceles triangle.
∴ ∠ABC = ∠ACB { ∴ AB = AC }∠ABC = 180° - 30° = 75° 2
XY || BC
∴ ∠AXY = ∠ABC = 75°
∴ ∠BXY = 180° – ∠ABC = 180° – 75° = 105°
- In ∆ABC, BD and CE are perpendicular to AC and AB respectively. If BD = CE, then ∆ ABC is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of a triangle ABC in which BD and CE are perpendicular to AC and AB respectively ,
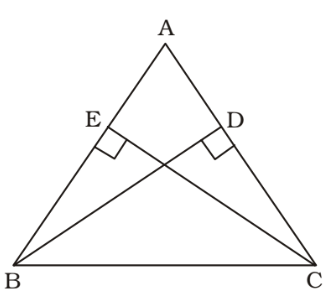
Area of ∆ ABC = 1 × AB × CE 2 Area of ∆ ABC = 1 × AC × BD 2
Correct Option: B
As per the given in question , we draw a figure of a triangle ABC in which BD and CE are perpendicular to AC and AB respectively ,

Area of ∆ ABC = 1 × AB × CE 2 Area of ∆ ABC = 1 × AC × BD 2
⇒ AB = AC [∵BD = CE]
∴ ∆ ABC is an isosceles triangle.
- ABC is an isosceles triangle such that AB = AC and AD is the median to the base BC with ∠ABC = 35°. Then ∠BAD is
-
View Hint View Answer Discuss in Forum
On the basis of given in question , we draw a figure of an isosceles triangle ABC ,
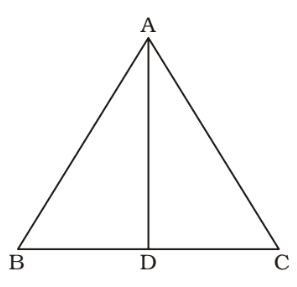
Given , AB = AC and BD = DC
∴ ∠ADB = ∠ADC = 90°
∠ABC = 35°
In ∆ ABD,Correct Option: B
On the basis of given in question , we draw a figure of an isosceles triangle ABC ,

Given , AB = AC and BD = DC
∴ ∠ADB = ∠ADC = 90°
∠ABC = 35°
In ∆ ABD,
∠BAD + ∠ABD = 90°
∴ ∠BAD = 90° – 35° = 55°

