Plane Geometry
- If one angle of a triangle is equal to half the sum of the other two equal angles, then the triangle is:
-
View Hint View Answer Discuss in Forum
Let one angle of the triangle be x°.
We know that , Sum of three angles of triangle = 180°
∴ Sum of remaining two angles = 180° – x
According to the question,x = 180° - x 2
Correct Option: C
Let one angle of the triangle be x°.
We know that , Sum of three angles of triangle = 180°
∴ Sum of remaining two angles = 180° – x
According to the question,x = 180° - x 2
⇒ 2x + x = 180°
⇒ 3x = 180°
⇒ x = 60°
∴ Other each angle = 60°
- G is the centroid of the equilateral triangle ABC. If AB = 9 cm, then AG is equal to
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of an equilateral triangle ABC

AD = √3 × Side 2 AD = √3 × 9 = 9√3 cm. 2 2
Correct Option: A
As per the given in question , we draw a figure of an equilateral triangle ABC

AD = √3 × Side 2 AD = √3 × 9 = 9√3 cm. 2 2 ∴ AG = 2 AD = 2 × 9√3 cm. 3 3 2
AG = 3√3cm.
- The lengths of the sides of a triangle are a, b and c respectively. If a² + b² + c² = ab + bc + ca, then the triangle is :
-
View Hint View Answer Discuss in Forum
Here , a² + b² + c² = ab + bc + ca
⇒ 2a² + 2b² + 2c² = 2ab + 2bc + 2ca
⇒ a² + b² – 2ab + b² + c² – 2bc + c² + a²– 2ca = 0
⇒ (a – b)² + (b – c)² + (c – a)² = 0
∴ a – b = 0 ⇒ a = b
b – c = 0 ⇒ b = c
c – a = 0 ⇒ c = aCorrect Option: B
Here , a² + b² + c² = ab + bc + ca
⇒ 2a² + 2b² + 2c² = 2ab + 2bc + 2ca
⇒ a² + b² – 2ab + b² + c² – 2bc + c² + a²– 2ca = 0
⇒ (a – b)² + (b – c)² + (c – a)² = 0
∴ a – b = 0 ⇒ a = b
b – c = 0 ⇒ b = c
c – a = 0 ⇒ c = a
∴ a = b = c
∴ It is an equilateral triangle.
- Internal bisectors of ∠Q and ∠R of ∆PQR intersect at O. If ∠ROQ = 96° then the vlaue of ∠RPQ is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of triangle ABC
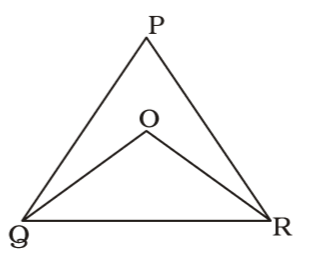
∠ROQ = 96°
In ∆ OQR
∠OQR + ∠ORQ + ∠QOR = 180°⇒ 1 ∠PQR + 1 ∠PRQ + 96° = 180° 2 2 ⇒ 1 (∠PQR + ∠PRQ) = 180° – 96° = 84° 2
Correct Option: C
As per the given in question , we draw a figure of triangle ABC

∠ROQ = 96°
In ∆ OQR
∠OQR + ∠ORQ + ∠QOR = 180°⇒ 1 ∠PQR + 1 ∠PRQ + 96° = 180° 2 2 ⇒ 1 (∠PQR + ∠PRQ) = 180° – 96° = 84° 2
⇒ ∠PQR + ∠PRQ = 2 × 84° = 168°
In ∆ PQR,
∴ ∠QPR = 180° – ( ∠PQR + ∠PRQ ) = 180° – 168° = 12°
- In ∆ABC, PQ is parallel to BC. If AP : PB = 1 : 2 and AQ = 3 cm; AC is equal to
-
View Hint View Answer Discuss in Forum
Firstly , We draw a figure of triangle ABC ,
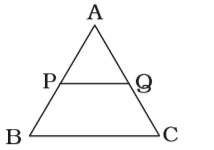
Here , AP : PB = 1 : 2AP = AQ = 1 PB QC 2
Correct Option: B
Firstly , We draw a figure of triangle ABC ,

Here , AP : PB = 1 : 2AP = AQ = 1 PB QC 2 ⇒ QC = 2 ⇒ QC + AQ = 3 AQ 1 AQ 1
⇒ AC = 3AQ = 9 cm

