Internal bisectors of ∠Q and ∠R of ∆PQR intersect

Home » Aptitude » Plane Geometry » Question

Internal bisectors of ∠Q and ∠R of ∆PQR intersect at O. If ∠ROQ = 96° then the vlaue of ∠RPQ is

As per the given in question , we draw a figure of triangle ABC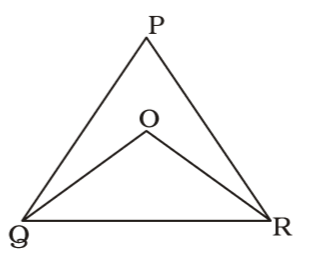

∠ROQ = 96°
In ∆ OQR
∠OQR + ∠ORQ + ∠QOR = 180°

⇒	1	∠PQR +	1	∠PRQ + 96° = 180°
	2		2

⇒	1	(∠PQR + ∠PRQ) = 180° – 96° = 84°
	2

⇒ ∠PQR + ∠PRQ = 2 × 84° = 168°
In ∆ PQR,
∴ ∠QPR = 180° – ( ∠PQR + ∠PRQ ) = 180° – 168° = 12°