On the basis of given in question , we draw a figure triangle ABC ,

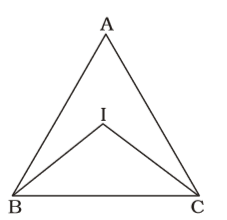
∠B + ∠C = 180 – 50 = 130°
In ∠BIC,
∠IBC + ∠ICB + ∠BIC = 180°

Correct Option: B

On the basis of given in question , we draw a figure triangle ABC ,

∠B + ∠C = 180 – 50 = 130°
In ∠BIC,
∠IBC + ∠ICB + ∠BIC = 180°

Firstly , We draw a figure of triangle ABC whose AD, BE and CF are medians ,

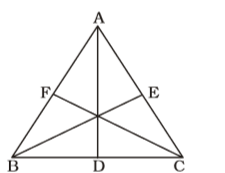
Points D, E, F are midpoints of BC, CA and AB respectively.
Any two sides of a triangle are together greater than twice the median drawn to the third side.
∴ AB + AC > 2AD
AB + BC > 2BE
BC + CA > 2CF
On adding, we get

Correct Option: A

Firstly , We draw a figure of triangle ABC whose AD, BE and CF are medians ,

Points D, E, F are midpoints of BC, CA and AB respectively.
Any two sides of a triangle are together greater than twice the median drawn to the third side.
∴ AB + AC > 2AD
AB + BC > 2BE
BC + CA > 2CF
On adding, we get
2 (AB + BC + CA) > 2 (AD + BE + CF)
∴ AB + BC + CA > AD + BE + CF

As per the given in question , we draw a figure of triangle ABC ,

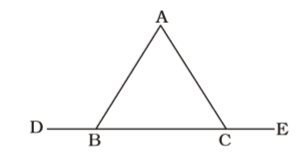
∠ABD = 120°
∴ ∠ABC = 180° – 120° = 60°
∠ACE = 105°

Correct Option: C

As per the given in question , we draw a figure of triangle ABC ,

∠ABD = 120°
∴ ∠ABC = 180° – 120° = 60°
∠ACE = 105°
⇒ ∠ACB = 180° – 105° = 75°
∴ ∠BAC = 180° – 60° – 75° = 45°

Here , ∠ABC = 5 ∠ACB and ∠BAC = 3∠ACB
We know that , ∠ABC + ∠ACB + ∠BAC = 180°

Correct Option: C

Here , ∠ABC = 5 ∠ACB and ∠BAC = 3∠ACB
We know that , ∠ABC + ∠ACB + ∠BAC = 180°

On the basis of given in question , we draw a figure triangle ABC ,

O = Orthocentre

Correct Option: D

On the basis of given in question , we draw a figure triangle ABC ,

From figure it is clear that the perpendiculars drawn from the vertices to the opposite sides of a triangle, meet at the point whose name is Orthocentre .