In ∆ ABC, the internal bisectors of ∠ABC and ∠ACB

Home » Aptitude » Plane Geometry » Question

In ∆ ABC, the internal bisectors of ∠ABC and ∠ACB meet at I and ∠BAC = 50°. The measure of ∠BIC is

On the basis of given in question , we draw a figure triangle ABC ,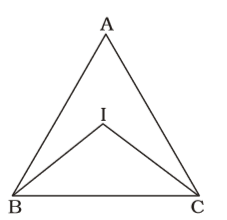

∠B + ∠C = 180 – 50 = 130°
In ∠BIC,
∠IBC + ∠ICB + ∠BIC = 180°

⇒	∠B	+	∠C	+ ∠BIC = 180°
	2		2

⇒ ∠BIC = 180° -	1	(∠B +∠C)
	2

∠BIC = 180° -	130
	2

∠BIC = 180° – 65° = 115°