-
The side AB of a parallelogram ABCD is produced to E in such way that BE = AB. DE intersects BC at Q. The point Q divides BC in the ratio
-
- 1 : 2
- 1 : 1
- 2 : 3
- 2 : 1
- 1 : 2
Correct Option: B
On the basis of question we draw a figure of parallelogram ABCD in which side AB is produced to E in such way that BE = AB. DE intersects BC at Q , 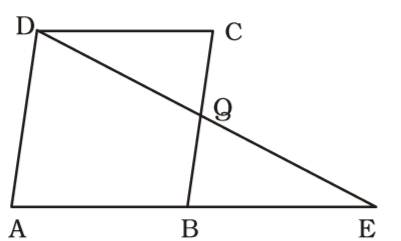
AD || BC ⇒ AD || BQ
Point B is the mid-point of AE.
∴ Q is the mid-point of DE.
In &8710;s DQC and BQE,
∠DQC = ∠BQE
∠DCQ = ∠QBE
∠CDQ = ∠QEB
∴ Both triangles ∆ DQC and ∆ BQE are similar.
| ∴ | = | = 1 : 1 | ||
| QE | BQ |

