Let O be the in-centre of a triangle ABC and D be a point

Home » Aptitude » Plane Geometry » Question

Let O be the in-centre of a triangle ABC and D be a point on the side BC of ∆ABC, such that OD ⊥ BC. If ∠BOD = 15°, then ∠ABC =

1. 75°
2. 45°
3. 150°
4. 90°

Correct Option: C

Firstly , We draw a figure of triangle ABC whose O be the in-centre ,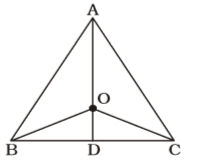

BO is the internal bisector of ∠B
∠ODB = 90°; ∠BOD = 15°
∴ ∠OBD = 180° – 90° – 15° = 75°
⇒ ∠ABC = 2 × 75° = 150°