-
O and C are respectively the orthocentre and circumcentre of an acute-angled triangle PQR. The points P and O are joined and produced to meet the side QR at S. If ∠PQS = 60° and ∠QCR = 130°, then ∠RPS=
-
- 30°
- 35°
- 100°
- 60°
- 30°
Correct Option: B
On the basis of given in question , we draw a figure with O and C are respectively orthocentre and circumcentre of an acute-angled triangle PQR ,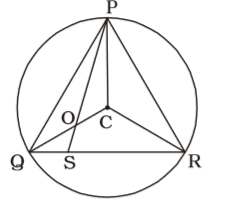
∠ PQS = 60°
∠ QCR = 130°
| ∴ ∠QPR = | × 130° = 65° | 2 |
⇒ ∠QRP =180° – 60° – 65° = 55°
⇒ ∠PCQ = 110°
∴ In ∆ QCR,
QC = CR
⇒ ∠CQR = ∠CRQ = 25°
[∵ ∠CQR + ∠CRQ = 50°]
∴ ∠PQC = ∠QPC = 35°
[∵ ∠PQC + ∠QPC = 70°]
Similarly, ∠ CPR = 30°
∴ ∠RPS = 35°

